Question: For each given matrix A, find a matrix P such that P'1AP is diagonal. 0' = [.62 13] (it) A = L63 12] (in) [21
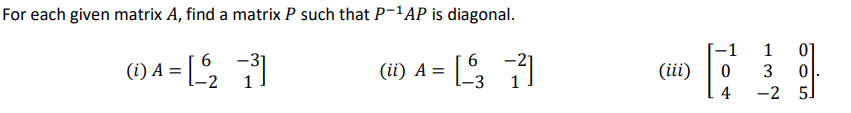
![P'1AP is diagonal. 0'\" = [.62 13] (it) A = L63 12]](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/10/6709aee0c8aee_8406709aee0b0a61.jpg)
For each given matrix A, find a matrix P such that P'1AP is diagonal. 0'\" = [.62 13] (it) A = L63 12] (in) [21 :2 E] 2 Lo O_ - A 4 O NI- (2] The eigenvectors (-2, 1) and (1, 2) form an orthogonal basis for R2. Normalize these eigenvectors to produce an orthonormal basis. - 2, 1) (1, 2) PI P2 |1 (1, 2)11 3. Each eigenvalue has a multiplicity of 1, so go directly to step 4. 4. Using p, and P2 as column vectors, construct the matrix P. P Verify that P orthogonally diagonalizes A by finding P-'AP = PTAP. IN PTAP = = o NO
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


