for more understanding clear steps is helpful thank you

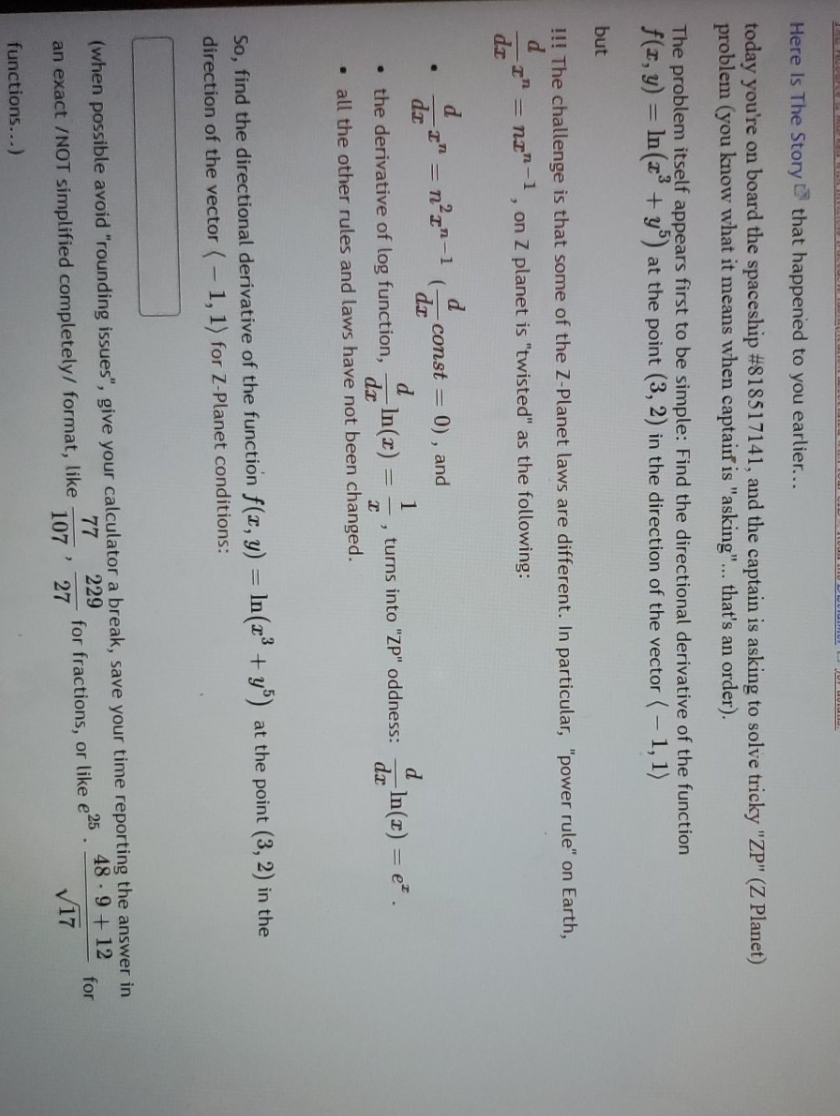
Here Is The Story that happened to you earlier... today you're on board the spaceship #818517141, and the captain is asking to solve tricky "ZP" (Z Planet) problem (you know what it means when captainf is "asking"... that's an order). The problem itself appears first to be simple: Find the directional derivative of the function f(x, y) = In(x + y ) at the point (3, 2) in the direction of the vector ( - 1, 1) but !!! The challenge is that some of the Z-Planet laws are different. In particular, "power rule" on Earth, di In = n" , on Z planet is "twisted" as the following: -I" = n210-1 -const = 0) , and . the derivative of log function, In(x) = - , turns into "ZP" oddness: In(x) = ez . all the other rules and laws have not been changed. So, find the directional derivative of the function f(x, y) = In( + y) at the point (3, 2) in the direction of the vector ( - 1, 1) for Z-Planet conditions: (when possible avoid "rounding issues", give your calculator a break, save your time reporting the answer in an exact / NOT simplified completely/ format, like for fractions, or like 25 . 48 - 9 + 12 for 107 ' 27 functions...)