For the first answer I got the correct result for g(x,y)= x-sqrt(y). However, I'm having a hard to get to the others.

Thank you

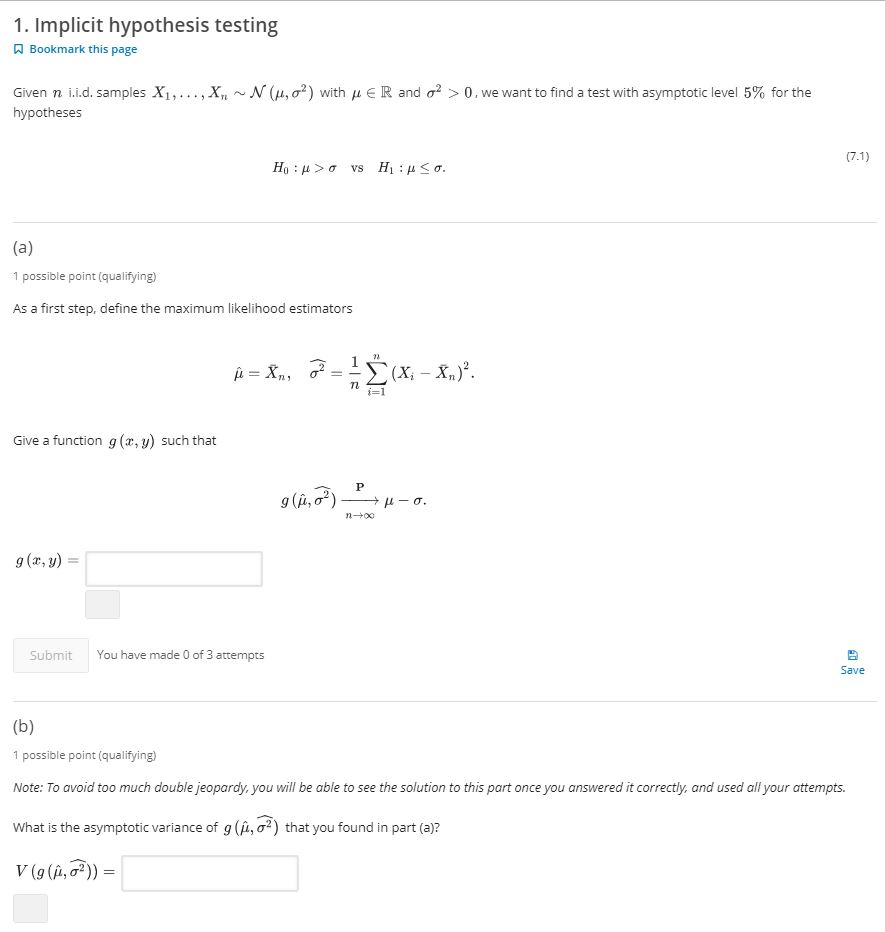
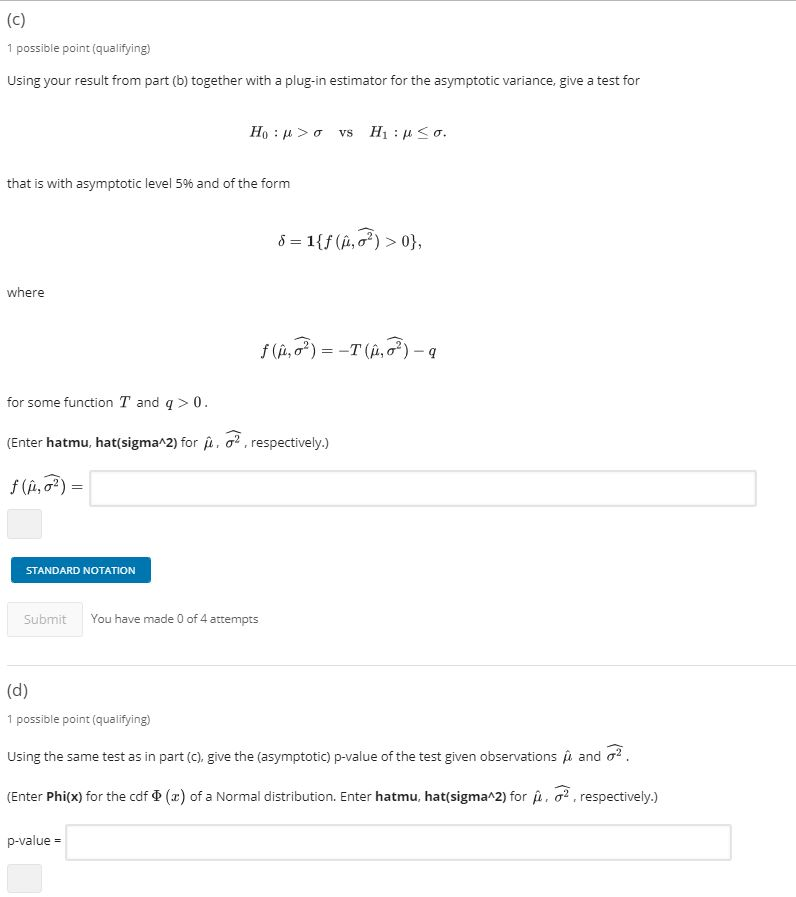
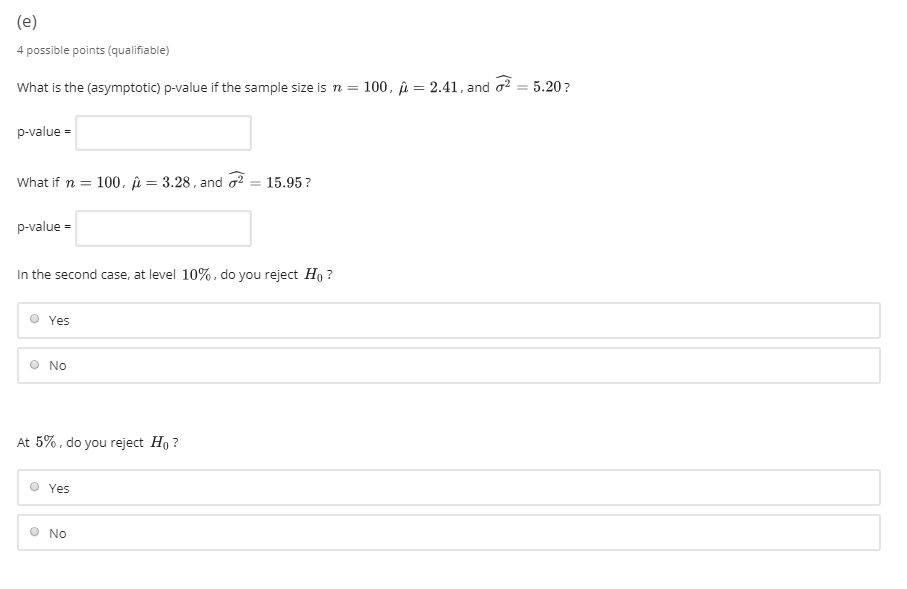
1. Implicit hypothesis testing @Bookmark this page Given n i.i.d. samples X1, . . ., Xn ~N (#, 02) with / E IR and o2 > 0. we want to find a test with asymptotic level 5% for the hypotheses Ho : # >0 vs H1 : uSo. (7.1) (a) 1 possible point (qualifying) As a first step, define the maximum likelihood estimators i - Xn, o= (X, - Xn)? Give a function g (x, y) such that g(i,?) -Pu -0. g (x, y) = Submit You have made 0 of 3 attempts Save (b) 1 possible point (qualifying) Note: To avoid too much double jeopardy, you will be able to see the solution to this part once you answered it correctly, and used all your attempts. What is the asymptotic variance of g (/1, 02) that you found in part (a)? V (g (/, G? ) ) =( C ) 1 possible point ( qualifying* Using your result from part ( b ) together with a plug - in estimator for the asymptotic variance , give a test for HO : MS O VS HI: HE`. that is with asymptotic level 546 and of the form* Where $ ( 1 , 0} ) = - [ (^ 03 1 - 9 for some function I' and ` = 0 . [Enter hatmu , hat ( sigman zy for $1 . 2 , respectively . ] f (1 , 0? ) = Submit* "You have made O of 4 attempts (d) I possible point (qualifying" Using the Same test as in part [ [ ). give the [asymptotic ; p-value of the test given observations { and } ? " [ Enter Philx ) for the calf* ( * ) of a Normal distribution . Enter hatmu , hat ( sigman 2 ) for $1 , 1 2 , respectively . ] p -value =( E ) 4 possible points ( qualifiable ) What is the [asymptotic ; p- value if the Sample Size is * = 100 , $1 = 2. 11 , and +2 - 5.20 ? p -value = What if 1 = 100, 1 = 3.28 , and 12 - 15.05 ? D - value = In the second case , at level 10 % , do you reject {In ?" ` YES O NO At 5 /0 , do you reject HIN ?! ` YES O NO