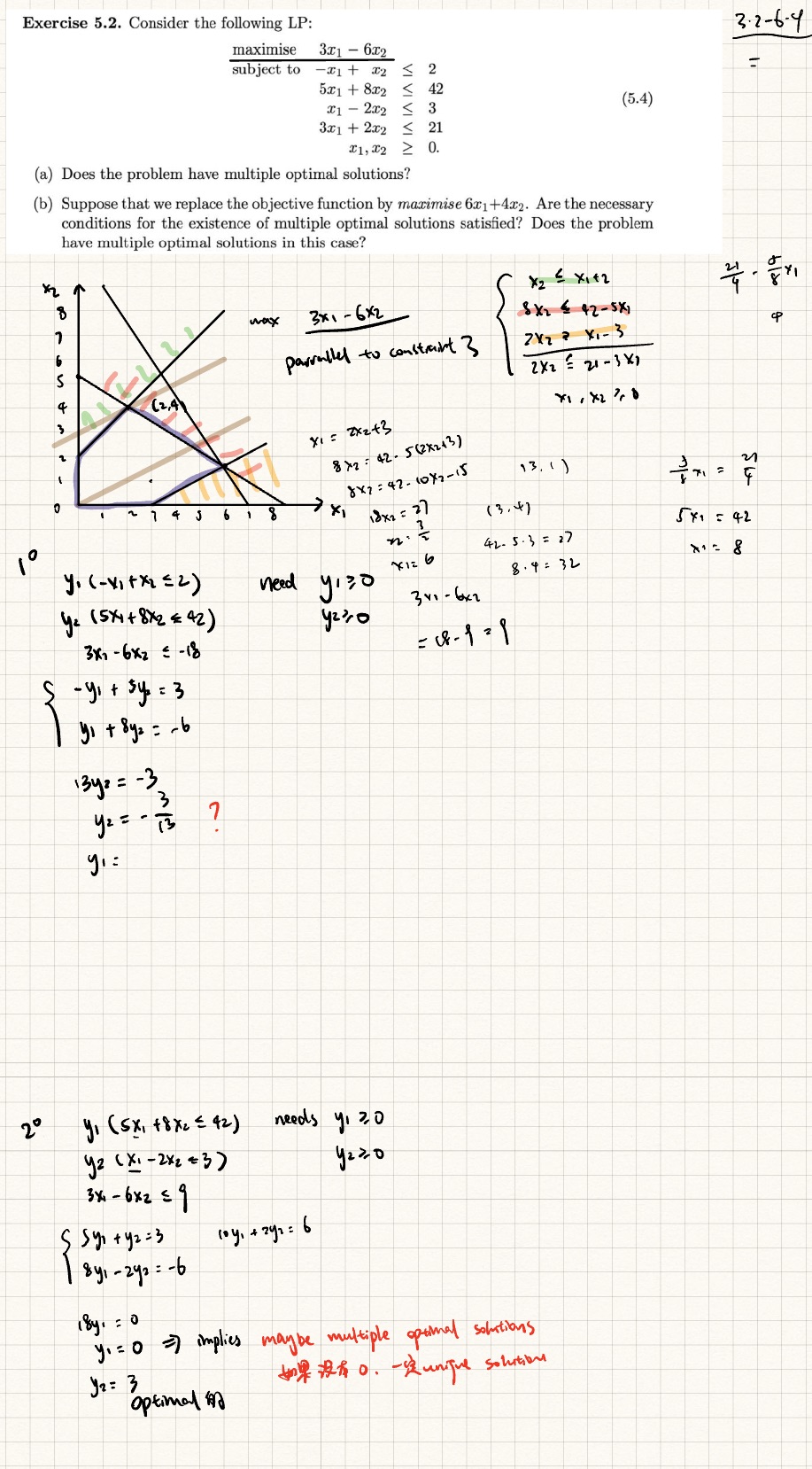
Question: For the first case do I get y2 correctly and how do I prove if there are multiple optimal solutions Exercise 5.2. Consider the following
For the first case do I get y2 correctly and how do I prove if there are multiple optimal solutions
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


