Question: - For the first year, the APR is 7% compounded monthly, so the monthly interest rate (r1) is 7%/12 = 0.58333% - For the second
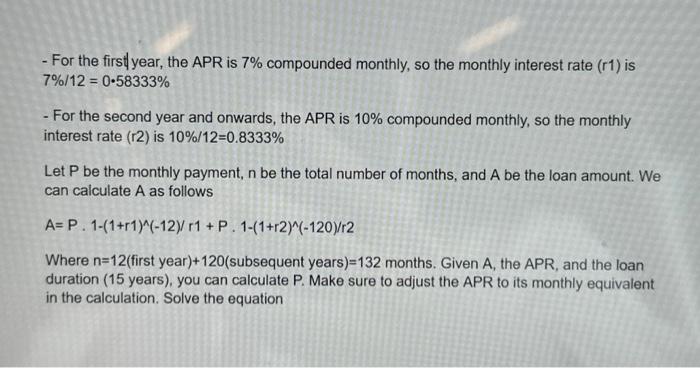
- For the first year, the APR is 7% compounded monthly, so the monthly interest rate (r1) is 7%/12=058333% - For the second year and onwards, the APR is 10% compounded monthly, so the monthly interest rate (r2) is 10%/12=0.8333% Let P be the monthly payment, n be the total number of months, and A be the loan amount. We can calculate A as follows A=P1(1+r1)(12)/r1+P1(1+r2)(120)/r2 Where n=12 (first year) +120 (subsequent years) =132 months. Given A, the APR, and the loan duration (15 years), you can calculate P. Make sure to adjust the APR to its monthly equivalent in the calculation. Solve the equation
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


