For the following java code segment, give a theoretical analysis of the running time.

sum = 0;

for(i = 0; i n; i = i + 1){

for(j = 0; j i * i; j = j + 1){

for(k = 0; k j; k = k + 1){

sum = sum + 1;

}

}

}

Hint:

1. The number of primitive operations of for(i = 0; i n; i = i + 1) =
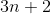
2. The number of primitive operations of for(j = 0; j i * i; j = j + 1) =
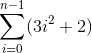
3. The number of primitive operations of for(k = 0; k j; k = k + 1) =
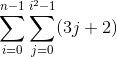
4. Compute the number of primitive operations for other statements.
5. Add them together as a function of n. You may need the following formulas:
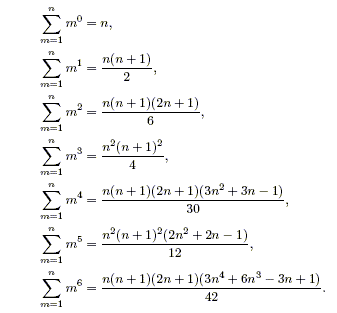
6. Apply the rules (change non-zero coefficient to 1; drop lower order terms) to simplify the function.

? = , m=1 ' - 0+11, ( + 1) 2 ( + 1) (2n + 1) ?. 6 m=1 - +11 - 1 ?( + 1)? 4 ( + 1)(2n + 1)(3n? + 3 1) 30 m=1 n?(n + 1)?(2n + 20 1), in 12 m=1 R ( + 1)(2n + 1)(374 +- 6n3 - 3 + 1) 42 m1