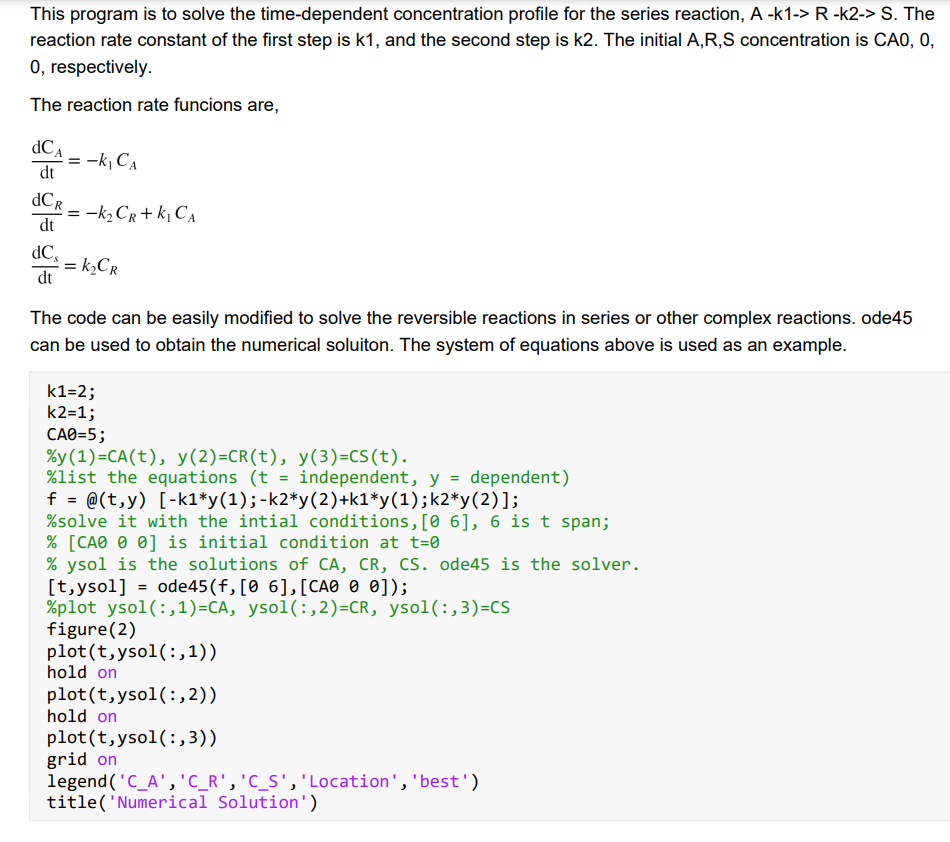
For the parallel elementary gaseous reactions below in a constant-volume batch reactor with the given values for the parameters, kqaz kgan A + B+C and 2A D A,1 Kpaz kfA,1 kbA,1 kfaz Kpaz = 5.0 with the proper units of mole of A, B, and C, liter and minutes. = 1.0 with the proper units of mole of A, B, and C, liter and minutes. 5.0 with the proper units of mole of A and D, liter and minutes. = 1.0 with the proper units of mole of A and D, liter and minutes. CA= 5.0 mole/liter (pure feed) 1) Give the equations for the net rate of consumption for A, B, C, and D. 2) Give the material balance equations for A, B, C, and D in terms of CA, CB, Cc, and Cd. See Part 3, page 3-10 for guidance. 3) Update your Mathlab code in Problem 1 to solve the equations in question 2 above to get the CA, CB, Cc, and Co versus time profiles with time long enough to show a good trend for all four profiles, like 6 minutes. This program is to solve the time-dependent concentration profile for the series reaction, A-k1-> R-k2-> S. The reaction rate constant of the first step is k1, and the second step is k2. The initial A,R,S concentration is CAO, O, O, respectively. The reaction rate funcions are, = CA = -k, CA dt DCR = -kz Cr+k, CA dt dC =k_CR dt = The code can be easily modified to solve the reversible reactions in series or other complex reactions. ode45 can be used to obtain the numerical soluiton. The system of equations above is used as an example. k1=2; k2=1; CAO=5; %y(1)=CA(t), y(2)=CR(t), y(3)=CS(t). %list the equations (t = independent, y = dependent) f = @(t,y) [-k1*y(1);-k2*y(2)+k1*y(1);k2*y(2)]; %solve it with the intial conditions, [06], 6 is t span; % [CAO O 0] is initial condition at t=0 % ysol is the solutions of CA, CR, Cs. ode45 is the solver. [t,ysol] = ode45(f,[0 6],[CAO 0 0]); %plot ysol(:,1)=CA, ysol(:,2)=CR, ysol(:,3)=CS figure(2) plot(t,ysol(:,1)) hold on plot(t,ysol(:,2)) hold on plot(t,ysol(:,3)) grid on legend('C_A', 'C_R', 'C_S', 'Location', 'best') title('Numerical Solution')