Question: For the problem below, find the range of optimality for the coefficient of x 2 (i.e., 'B' in this case). That is, produce the 5-step
For the problem below, find the range of optimality for the coefficient of x2 (i.e., 'B' in this case). That is, produce the 5-step procedure (re-produced below) that denotes the upper and lower limits of the range of optimality for the coefficient of 'B' in the objective function. Note, that you first must find the optimal solution to this problem. You will need to use substitution or simultaneous equations to find the explicit numeric values of the decision variables at the optimal solution.
Step 1: Find the slope of the objective function.
Step 2: Substitute an arbitrary coefficient for the coefficient of x2 in the objective function and find the slope.
Step 3: Find the slope of the first constraint involved at the optimal solution and set it equal to the slope of the objective function found in step 2.
Step 4: Find the slope of the second constraint involved at the optimal solution and set it equal to the slope of the objective function found in step 2.
Step 5: Express and interpret the complete sensitivity range for the coefficient of x2 in the objective function.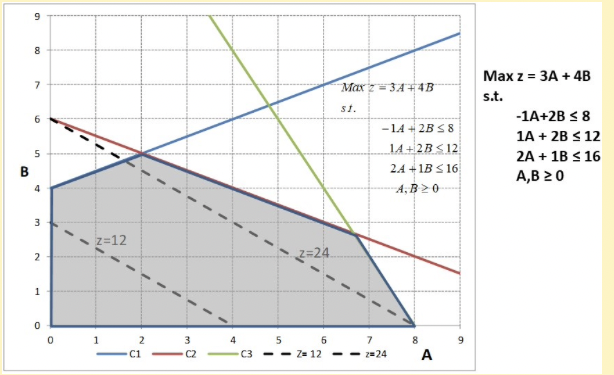
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


