For the system X'(1) = A. X(1) (1) Clarify by depending on the eigenvalues, of the matrix A that...

Transcribed Image Text:

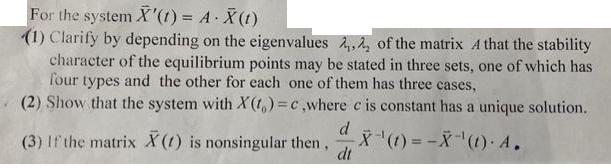
For the system X'(1) = A. X(1) (1) Clarify by depending on the eigenvalues, of the matrix A that the stability character of the equilibrium points may be stated in three sets, one of which has four types and the other for each one of them has three cases, (2) Show that the system with X(t)=c,where c is constant has a unique solution. (3) If the matrix X(t) is nonsingular then, -X (1)=-X¹ (1). A. d dt For the system X'(t) = A· X (1) (1) Clarify by depending on the eigenvalues of the matrix A that the stability character of the equilibrium points may be stated in three sets, one of which has four types and the other for each one of them has three cases, (2) Show that the system with X(t)=c,where c is constant has a unique solution. d (3) If the matrix X(t) is nonsingular then, -X (1)=-X¹ (1). A. dt

Answer rating: 100% (QA)

It seems like you re describing a system of linear differential equations possibly related to stabil View the full answer