Question: Let C' be a q-ary (n, M, 3)-code. Prove that the Hamming bound B =q/V(n, 1) is better (i.e., smaller) than the Singleton bound

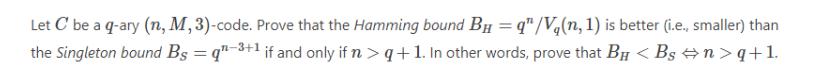
Let C' be a q-ary (n, M, 3)-code. Prove that the Hamming bound B =q"/V(n, 1) is better (i.e., smaller) than the Singleton bound Bs = q-3+1 if and only if n>q+1. In other words, prove that B q+1.

Step by Step Solution

★★★★★

3.39 Rating (155 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Answer i If a code has more than q plus one codeword it is recommende... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Accounting Questions!

Let C be a smooth C2 arc with parametrization (É¸, [a, b]), and suppose that s = ï¬(t) is given by (2). The natural parametrization of C is the pair (v, [0, L]), where v(s) =...

Let c be a persons cholesterol level (in mg/dl) after ingesting d milligrams of an experimental cholesterol drug each day for one month. Identify the explanatory and the response variables. Which...

Let C be a fixed n x n matrix. Determine whether the following are linear operators on R n n (a) L(A)= CA + AC (b) L(A) = C2A (c) L(A) = A2C

Given n Z+, let the set M(n, k) Zn2 contain the maximum number of code words of length n, where the minimum distance between code words is 2k + 1. Prove that (The upper bound on |M(n, k)| is called...

Let F be a continuous c.d.f. satisfying F(0) = 0, and suppose that the distribution with c.d.f. F has the memory less property (5.7.18). Define (x) = log[1 F(x)] for x > . a. Show that for all t, h >...

Use Theorem 27.24 to prove the equivalence of these two theorems: Fundamental Theorem of Algebra: Every nonconstant polynomial in C[x] has a zero in C. Nullstellensatz for C[x]: Let f 1 (x), , f r...

Exercise 5.1. Recall that a solution {x (t)}T t=0 to a dynamic optimization problem is timeconsistent if the following is true: whenever {x (t)}T t=0 is an optimal solution starting at time t = 0, {x...

[35] Let L = 12 ... be the characteristic sequence for language L {0, 1} such that i = 1 iff the lexicographically ith word wi is in L. As before, L 1,> 0. (c) There is a language L SPACE[2O(n)]...

15.5 Prove the following results about conditional means, forecasts, and forecast errors: a. Let W be a random variable with mean mW and variance s2 w, and let c be a constant. Show that E31W - c2 24...

Let X have the probability distribution show that the random variable Y = ?2 In A' has a chi-squared distribution with 2 degrees of freedom. 1. 0

If the future cash flows from an investment are not certain, then we call such an investment risky. And the more uncertain are those cash flows, the greater the risk. This means there is an...

Duncan Hines produces a boxed cake mix that features Toll House chocolate chips. This is an example of rebranding. Group of answer choices false true

One of the weaknesses of Feeding trials is that the diet consumption may not be quantified

On January 1, 2025, a new Board of Directors was elected for Cullumber Hospital. The new board switched to a different accountant. After reviewing the hospital's books, the accountant decided that...

Mark this question Find all asymptotes and/or holes in the graph of f(x)= 3 4x-9x 2x-x-3

Problem 3 (24 Points; 12 points each for (a)-(b)) Consider a material which has yielded according to the von Mises yield criterion with y = 40 ksi. The dilatational strain is 0.001, the Young's...

Slugging Baseball Co. buys and sells baseballs. They employ the weighted average method of inventory valuation. At the beginning of the year, Slugging Baseball Co. had 251 baseballs which had been...

QUESTION 9 HC-O-C-R R-C-O-CH HC-O-P-O-CH-CH-NH3* O || O a. Phosphatidic acid, Serine O b. Lysophosphatidic acid, Serine, Free FA O c. Lysophosphatidylserine, Free FA O d. 2 Free FAs, Serine, Glycerol...

Throughout this book, we assume that parameter passing during procedure calls takes constant time, even if an N-element array is being passed. This assumption is valid in most systems because a...

Suppose that we are given a set of n objects, where the size si of the i th object satisfies 0

Describe an efficient algorithm that, given a set x 1, x 2, . . . ,x n of points on the real line, determines the smallest set of unit-length closed intervals that contains all of the given points....

The part of the brain that coordinates voluntary movement and enables nonverbal learning and memory is the _______.

The _______ _______ secrete(s) epinephrine and norepinephrine, helping to arouse the body during times of stress.

In a sending neuron, when an action potential reaches an axon terminal, the impulse triggers the release of chemical messengers called _______.