For this problem, I need help with deriving the equation below with z = tanh(w^Tx). I've attached class notes for deriving the backpropagation algorithm where z = sigma_y. However, I need to derive with z = tanh.

PLEASE DO NOT COMMENT OR ANSWER IF YOU ARE UNABLE TO HELP OR PROVIDE USEFUL CLARIFICATION WITH INTENT TO ANSWER AFTER MY EDITING!!!

CLASS NOTES:

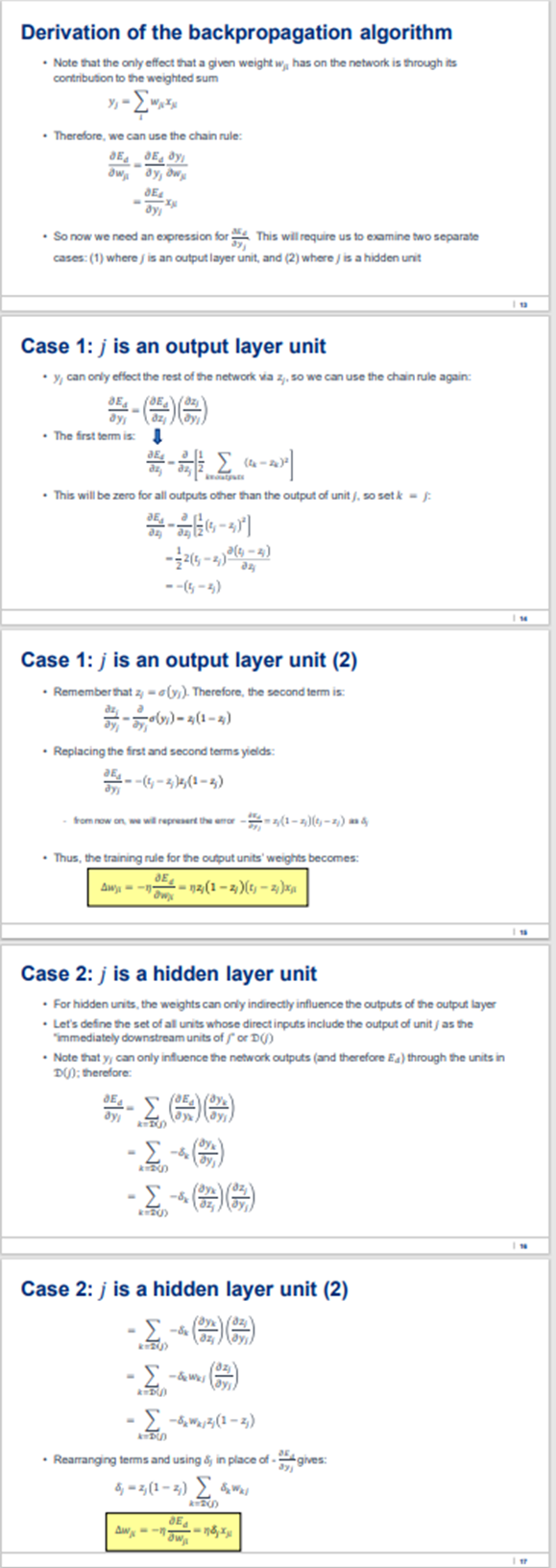
Using the sum of squared errors function E(w) = 2aEx{tka Zka), revise the Backpropagation algorithm for a two-class classification application so that it operates on units using the squashing" function tanh in place of the sigmoid function. That is, assume the output of a single unit is z = tanh(w+x). Give the weight update rule for output layer weights and hidden layer weights. Hint: tanh'(x) = 1 tanh2(x) Backpropagation . Let's start by redefining the error E to sum the errors over all of the network outputs: E(w) = [ { (txa Exa)? LED keoutputs where outputs is the set of output units in the network, tkd is the target value for the kth output unit and training example d, and Zed is the actual output of the kth output unit for training example d. Similarly, we can define the error Ed for a single training example as: Ea(w) == E (tx 2y)? keoutputs 11 Backpropagation (2) . Stochastic gradient descent involves iterating through the training examples one at a time . For each training example d, we descend the gradient of the error Ed with respect to this single example . Thus, for each training example d, every weight w;; is updated by adding Aw; to it Ea Awji = -aw We can derive an expression for Ed in order to implement the rule shown above aw Derivation of the backpropagation algorithm . Note that the only effect that a given weight w, has on the network is through its contribution to the weighted sum -. . Therefore, we can use the chain rule: DE BE, dy ow, oy, owy DE dy . So now we need an expression for This will require us to examine two separate cases: (1) where is an output layer unit, and (2) where is a hidden unit Case 1: j is an output layer unit y can only effect the rest of the network via 2, so we can use the chain rule again: DE The first termis 1 LE40-20 ( . This will be zero for all outputs other than the output of unit), so setk - hot (3) - {2(3-2) 019-31) --(-2) de Case 1: j is an output layer unit (2) . Remember that 2-cy). Therefore, the second term is: oly)=3(1-3) Replacing the first and second terms yields: E --(1-2), (1-2) - from now on, we will represent the ecz(1-2)(1)-2) Thus, the training rule for the output units' weights becomes: BE Awi - -- 13(1-2)0 - 2) dw Case 2: j is a hidden layer unit . For hidden units, the weights can only indirectly influence the outputs of the output layer Let's define the set of all units whose direct inputs include the output of unit as the immediately downstream units of or (b) . Note that y can only influence the network outputs (and therefore Ea) through the units in D(); therefore: dyy (86) (3) A -8, A0 20) Case 2: j is a hidden layer unit (2) -8 RU dz - -&us DO 2 -82,3(1-2) Rearranging terms and using 8, in place of gives: 8; -7/(1-2) W DU AWWA DE -15% Using the sum of squared errors function E(w) = 2aEx{tka Zka), revise the Backpropagation algorithm for a two-class classification application so that it operates on units using the squashing" function tanh in place of the sigmoid function. That is, assume the output of a single unit is z = tanh(w+x). Give the weight update rule for output layer weights and hidden layer weights. Hint: tanh'(x) = 1 tanh2(x) Backpropagation . Let's start by redefining the error E to sum the errors over all of the network outputs: E(w) = [ { (txa Exa)? LED keoutputs where outputs is the set of output units in the network, tkd is the target value for the kth output unit and training example d, and Zed is the actual output of the kth output unit for training example d. Similarly, we can define the error Ed for a single training example as: Ea(w) == E (tx 2y)? keoutputs 11 Backpropagation (2) . Stochastic gradient descent involves iterating through the training examples one at a time . For each training example d, we descend the gradient of the error Ed with respect to this single example . Thus, for each training example d, every weight w;; is updated by adding Aw; to it Ea Awji = -aw We can derive an expression for Ed in order to implement the rule shown above aw Derivation of the backpropagation algorithm . Note that the only effect that a given weight w, has on the network is through its contribution to the weighted sum -. . Therefore, we can use the chain rule: DE BE, dy ow, oy, owy DE dy . So now we need an expression for This will require us to examine two separate cases: (1) where is an output layer unit, and (2) where is a hidden unit Case 1: j is an output layer unit y can only effect the rest of the network via 2, so we can use the chain rule again: DE The first termis 1 LE40-20 ( . This will be zero for all outputs other than the output of unit), so setk - hot (3) - {2(3-2) 019-31) --(-2) de Case 1: j is an output layer unit (2) . Remember that 2-cy). Therefore, the second term is: oly)=3(1-3) Replacing the first and second terms yields: E --(1-2), (1-2) - from now on, we will represent the ecz(1-2)(1)-2) Thus, the training rule for the output units' weights becomes: BE Awi - -- 13(1-2)0 - 2) dw Case 2: j is a hidden layer unit . For hidden units, the weights can only indirectly influence the outputs of the output layer Let's define the set of all units whose direct inputs include the output of unit as the immediately downstream units of or (b) . Note that y can only influence the network outputs (and therefore Ea) through the units in D(); therefore: dyy (86) (3) A -8, A0 20) Case 2: j is a hidden layer unit (2) -8 RU dz - -&us DO 2 -82,3(1-2) Rearranging terms and using 8, in place of gives: 8; -7/(1-2) W DU AWWA DE -15%