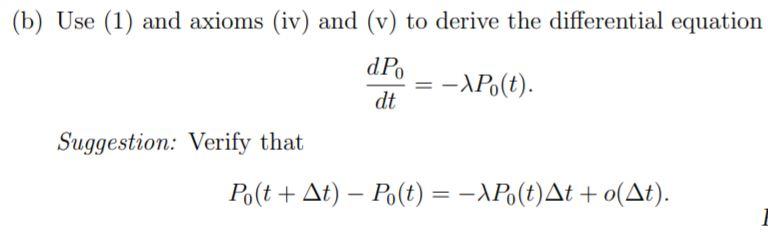FOR THIS PROBLEM PLEASE HELP SOLVE IT THE BEST WAY YOU CAN USING THE INFORMATION GIVEN. ANYTHING WILL HELP AND PLEASE SHOW IT NEATLY.

PROBLEM: WHATEVER YOU CAN SHOW ME WILL HELP

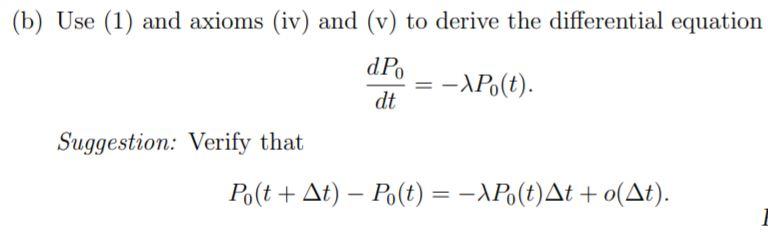
{M(t)|t>0}, to model occurrences of events at random points in time. Here M(t) counts the number of occurrences in the time interval [0, t). This continuous-time random process may also be defined as one satisfying the following axioms: (i) M(0) = 0. (ii) The number of events that occur in disjoint time intervals are independent; in symbols, for ti 0, M(t + s) M(t) depends only on s, so that Pr[M(t+s) M(t) = k] = Pr[M(s) M(0) = k], = for all k. (iv) Pr[M(At) = 1] = \At+o(At). (v) Pr[M(At) > 2) = o(At). The notation o(h) in (iv) and (v) is defined as follows: We say that an expression, f(h), is o(h) as h0 iff lim f(h) 0. h+0 h The constant in (iv) is called the rate of the process. Set Pm (t) = Pr[M(t) = m), for m = 0, 1, 2, 3 ..., and t > 0. Use the axioms (i)-(v) to prove the following assertions. (b) Use (1) and axioms (iv) and (v) to derive the differential equation dP dt = -\P.(t). Suggestion: Verify that Po(t + At) Po(t) = -\Po(t)At + o(At). {M(t)|t>0}, to model occurrences of events at random points in time. Here M(t) counts the number of occurrences in the time interval [0, t). This continuous-time random process may also be defined as one satisfying the following axioms: (i) M(0) = 0. (ii) The number of events that occur in disjoint time intervals are independent; in symbols, for ti 0, M(t + s) M(t) depends only on s, so that Pr[M(t+s) M(t) = k] = Pr[M(s) M(0) = k], = for all k. (iv) Pr[M(At) = 1] = \At+o(At). (v) Pr[M(At) > 2) = o(At). The notation o(h) in (iv) and (v) is defined as follows: We say that an expression, f(h), is o(h) as h0 iff lim f(h) 0. h+0 h The constant in (iv) is called the rate of the process. Set Pm (t) = Pr[M(t) = m), for m = 0, 1, 2, 3 ..., and t > 0. Use the axioms (i)-(v) to prove the following assertions. (b) Use (1) and axioms (iv) and (v) to derive the differential equation dP dt = -\P.(t). Suggestion: Verify that Po(t + At) Po(t) = -\Po(t)At + o(At)