Formulate an integer linear programming $($ILP$)$ model that solves for the production schedule over

the following six months. It is required to know how much units should be manufactured each

month, and at what configuration setting. Following your formulation, solve your ILP in the

mathematical programming code of your choosing. Following your formulation, solve your ILP in the mathematical programming code of your choosing.

Re$-$solve your model where the cost of holding stock is increased to R$60000\mathrm{.}00.$ This is to test how

sensitive your schedule is towards a large fluctuation in holding cost.

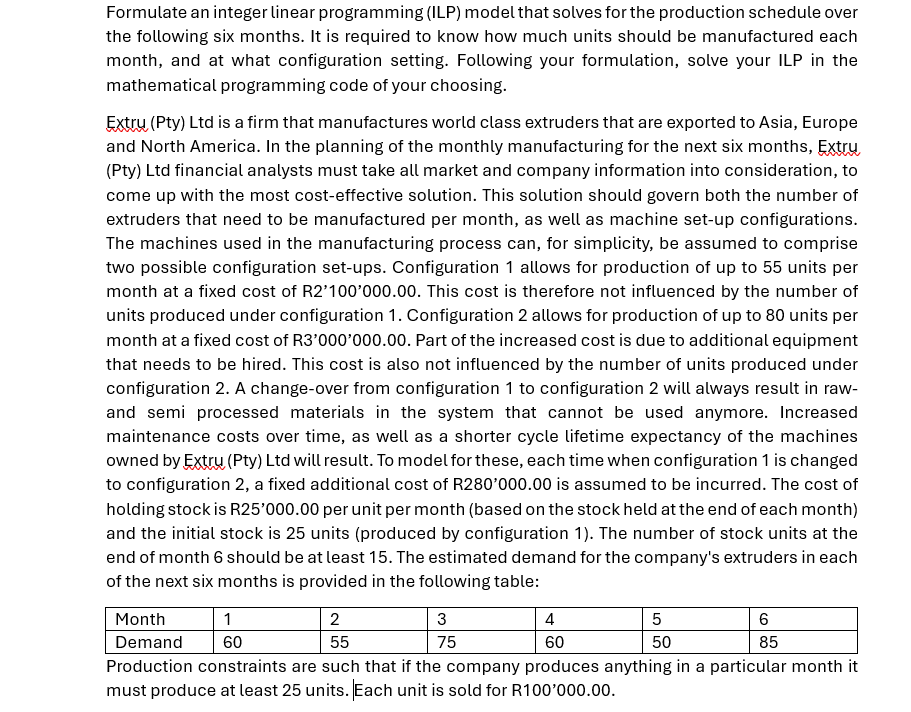
Extru $($Pty$)$ Ltd is a firm that manufactures world class extruders that are exported to Asia, Europe

and North America. In the planning of the monthly manufacturing for the next six months, Extru

$($Pty$)$ Ltd financial analysts must take all market and company information into consideration, to

come up with the most cost$-$effective solution. This solution should govern both the number of

extruders that need to be manufactured per month, as well as machine set$-$up configurations.

The machines used in the manufacturing process can, for simplicity, be assumed to comprise

two possible configuration set$-$ups. Configuration $1$ allows for production of up to $55$ units per

month at a fixed cost of R$2\text{'}100\text{'}000\mathrm{.}00.$ This cost is therefore not influenced by the number of

units produced under configuration $1.$ Configuration $2$ allows for production of up to $80$ units per

month at a fixed cost of R$3\text{'}000\text{'}000\mathrm{.}00.$ Part of the increased cost is due to additional equipment

that needs to be hired. This cost is also not influenced by the number of units produced under

configuration $2.$ A change$-$over from configuration $1$ to configuration $2$ will always result in raw$-$

and semi processed materials in the system that cannot be used anymore. Increased

maintenance costs over time, as well as a shorter cycle lifetime expectancy of the machines

owned by Extru $($Pty$)$ Ltd will result. To model for these, each time when configuration $1$ is changed

to configuration $2,$ a fixed additional cost of R$280\text{'}000\mathrm{.}00$ is assumed to be incurred. The cost of

holding stock is R$25\text{'}000\mathrm{.}00$ per unit per month $($based on the stock held at the end of each month$)$

and the initial stock is $25$ units $($produced by configuration $1).$ The number of stock units at the

end of month $6$ should be at least $15.$ The estimated demand for the company's extruders in each

of the next six months is provided in the following table:

Production constraints are such that if the company produces anything in a particular month it

must produce at least $25$ units. Each unit is sold for R$100\text{'}000\mathrm{.}00.$