• Formulate the Linear Program and discuss the variables used, objective function and constraints.

• Using the LP from (1) to determine what the total optimal costs for the current supply chain.

• Suppose that the company is willing to drop distribution center restrictions. What customers could be served by any of the distribution centers for which costs are available. Can overall company costs be reduced? If so, by how much?

• Examine how a direct to customer solution strategy would work. Assume that it will costs $0.30 per unit to hip from San Bernardino to Los Angeles and $0.70 from San Bernardino to San Diego. Further assume that it will costs $3.50 for directs shipments from El Paso to San Antonio. How would these changes effect overall costs? Should we consider this strategy?

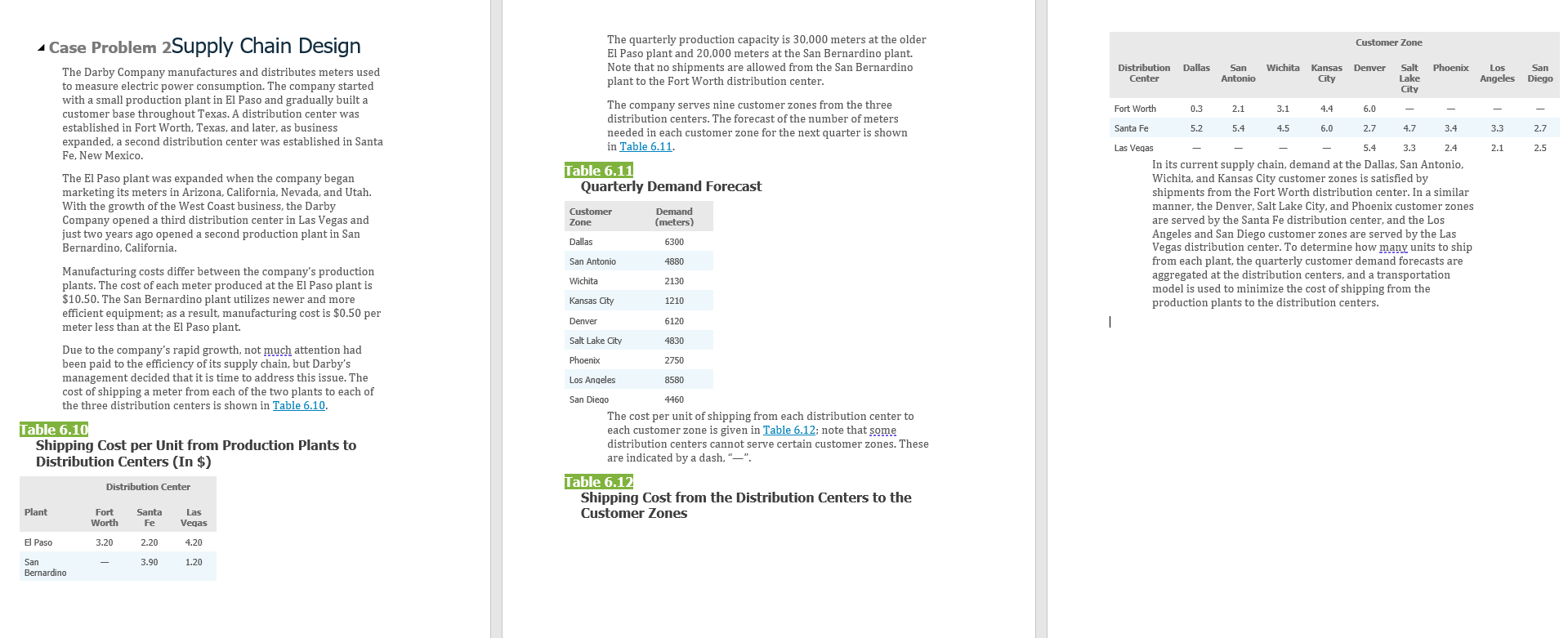
* Case Problem 2Supply Chain Design The Darby Company manufactures and distributes meters used to measure electric power consumption. The company started with a small production plant in El Paso and gradually built a customer base throughout Texas. A distribution center was established in Fort Worth, Texas, and later, as business expanded, a second distribution center was established in Santa Fe, New Mexico. The El Paso plant was expanded when the company began marketing its meters in Arizona, California, Nevada, and Utah. With the growth of the West Coast business, the Darby Company opened a third distribution center in Las Vegas and just two years ago opened a second production plant in San Bernardino, California. Manufacturing costs differ between the company's production plants. The cost of each meter produced at the El Paso plant is $10.50. The San Bernardino plant utilizes newer and more efficient equipment; as a result, manufacturing cost is $0.50 per meter less than at the El Paso plant. Due to the company's rapid growth, not much attention had been paid to the efficiency of its supply chain, but Darby's management decid that it is time to add this issue. The cost of shipping a meter from each of the two plants to each of the three distribution centers is shown in Table 6.10. Table 6.10 Shipping Cost per Unit from Production Plants to Distribution Centers (In $) Distribution Center Plant Santa Fe El Paso 2.20 San 3.90 Bernardino Fort Worth 3.20 Las Vegas 4.20 1.20 The quarterly production capacity is 30,000 meters at the older El Paso plant and 20,000 meters at the San Bernardino plant. Note that no shipments are allowed from the San Bernardino plant to the Fort Worth distribution center. The company serves nine customer zones from the three distribution centers. The forecast of the number of meters needed in each customer zone for the next quarter is shown in Table 6.11. Table 6.11 Quarterly Demand Forecast Customer Demand Zone (meters) Dallas 6300 San Antonio 4880 Wichita 2130 Kansas City 1210 Denver 6120 Salt Lake City 4830 Phoenix 2750 Los Angeles 8580 San Diego 4460 The cost per unit of shipping from each distribution center to each customer zone is given in Table 6.12; note that some distribution centers cannot serve certain customer zones. These are indicated by a dash, "-". Table 6.12 Shipping Cost from the Distribution Centers to the Customer Zones Customer Zone Distribution Dallas San Wichita Kansas Denver Salt Phoenix Center Antonio City Lake City Los San Angeles Diego Fort Worth 0.3 Santa Fe 5.2 2.1 3.1 5.4 4.5 4.4 6.0 6.0 2.7 3.3 2.7 4.7 3.3 3.4 2.4 Las Vegas 5.4 2.1 2.5 In its current supply chain, demand at the Dallas, San Antonio, Wichita, and Kansas City customer zones is satisfied by shipments from the Fort Worth distribution center. In a similar manner, the Denver, Salt Lake City, and Phoenix customer zones are served by the Santa Fe distribution center, and the Los Angeles and San Diego customer zones are served by the Las Vegas distribution center. To determine how many units to ship from each plant, the quarterly customer demand forecasts are aggregated at the distribution centers, and a transportation model is used to minimize the cost of shipping from the production plants to the distribution centers