From Chapter 3 - Functions and Algorithms; select one problem from the Solved Problemslist. Explain the problem and present the solution also explaining (in detail)each step and why the solution is correct.

After your main post, comment on submissions of at least two of your colleagues seeking clarification or providing further insights.

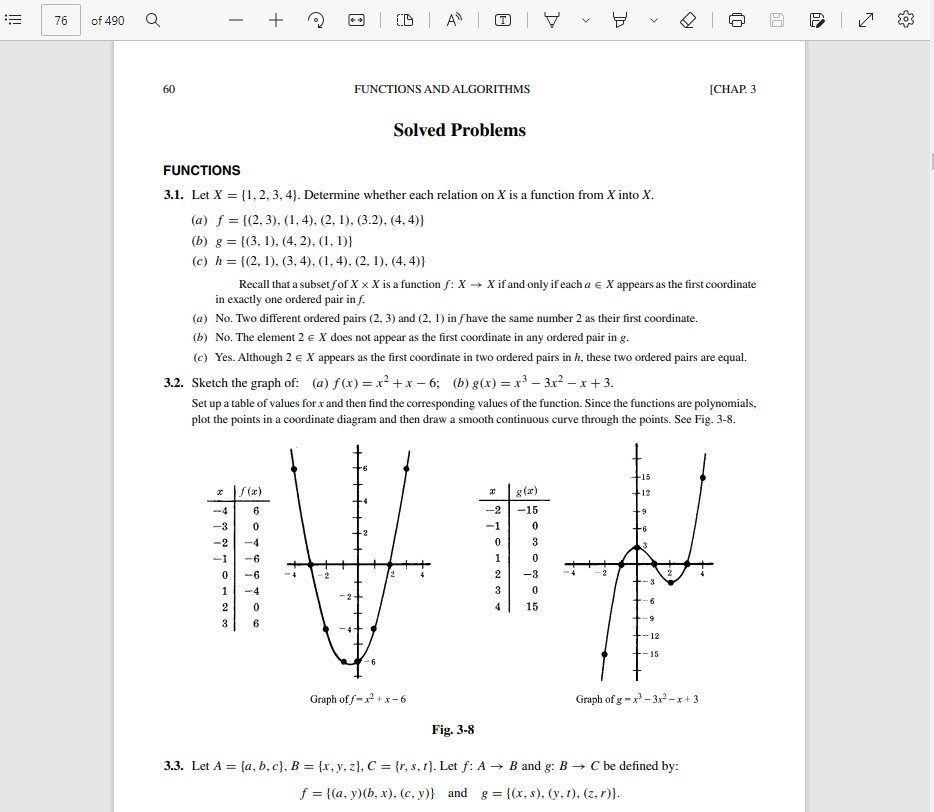
76 of 490 Q - + CL A | | V V E 60 FUNCTIONS AND ALGORITHMS [CHAP. 3 Solved Problems FUNCTIONS 3.1. Let X = [1, 2, 3, 4). Determine whether each relation on X is a function from X into X. (a) f = {(2, 3), (1, 4), (2, 1), (3.2), (4, 4)} (b) g = {(3, 1), (4, 2). (1, 1)} (c) h = {(2, 1), (3, 4), (1, 4), (2, 1), (4,4) } Recall that a subset fof X x X is a function f: X -> X if and only if each a e X appears as the first coordinate in exactly one ordered pair in f. (a) No. Two different ordered pairs (2, 3) and (2, 1) in fhave the same number 2 as their first coordinate. (b) No. The element 2 e X does not appear as the first coordinate in any ordered pair in g. (c) Yes. Although 2 6 X appears as the first coordinate in two ordered pairs in h, these two ordered pairs are equal. 3.2. Sketch the graph of: (a) f(x) = x-+x-6; (b) g(x) = x3- 3x2 -x+3. Set up a table of values for x and then find the corresponding values of the function. Since the functions are polynomials, plot the points in a coordinate diagram and then draw a smooth continuous curve through the points. See Fig. 3-8. S (x) -2 -15 - -12 Graph of f - 12 + x-6 Graph of g - x3 - 3x3 - x + 3 Fig. 3-8 3.3. Let A = (a, b, c), B = (x, y, z], C = {r, s, f). Let f: A - B and g: B - C be defined by: f = {(a, y)(b, x), (c, y)] and g = ((x, $), (y, 1), (z, r)]