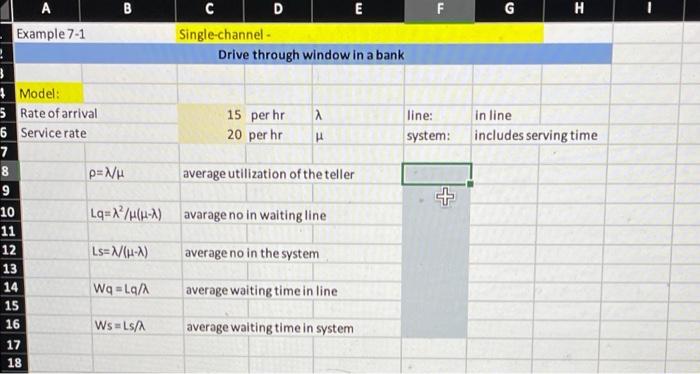
Question: G H A E Example 7-1 Single-channel - 2 Drive through window in a bank 3 + Model: 5 Rate of arrival 15 per hr
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


