Game theory

Question

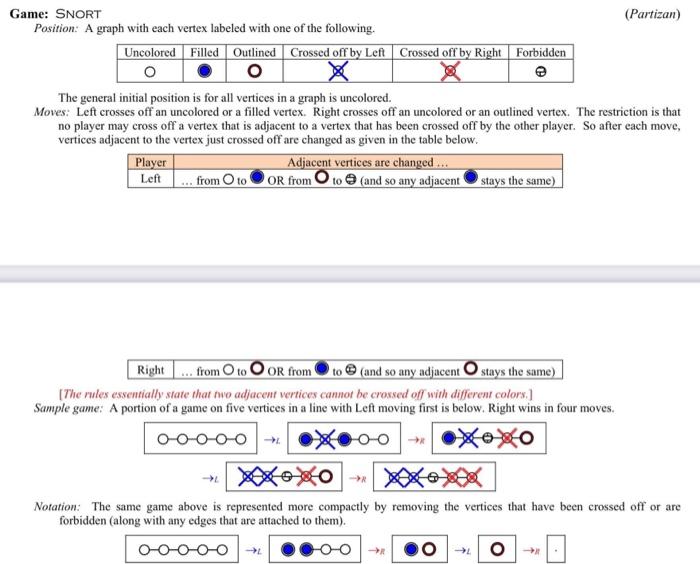
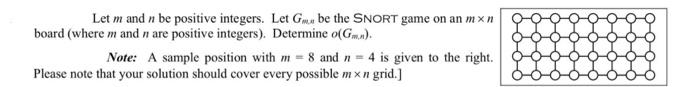
Game: SNORT (Parti Position: A graph with each vertex labeled with one of the following. [- The general initial position is for all vertices in a graph is uncolored. Moves: Left crosses off an uncolored or a filled vertex. Right crosses off an uncolored or an outlined vertex. The restriction is no player may cross off a vertex that is adjacent to a vertex that has been crossed off by the other player. So after each m vertices adjacent to the vertex just crossed off are changed as given in the table below. [The rules essentially state that no adjacent vertices cannot be crossed off with different colors.] Sample game: A portion of a game on five vertices in a line with Left moving first is below. Right wins in four moves. Notation: The same game above is represented more compactly by removing the vertices that have been crossed off or forbidden (along with any edges that are attached to them). Let m and n be positive integers. Let Gmub be the SNORT game on an mn board (where m and n are positive integers). Determine o(Gm,n). Note: A sample position with m=8 and n=4 is given to the right. Please note that your solution should cover every possible mn grid.]