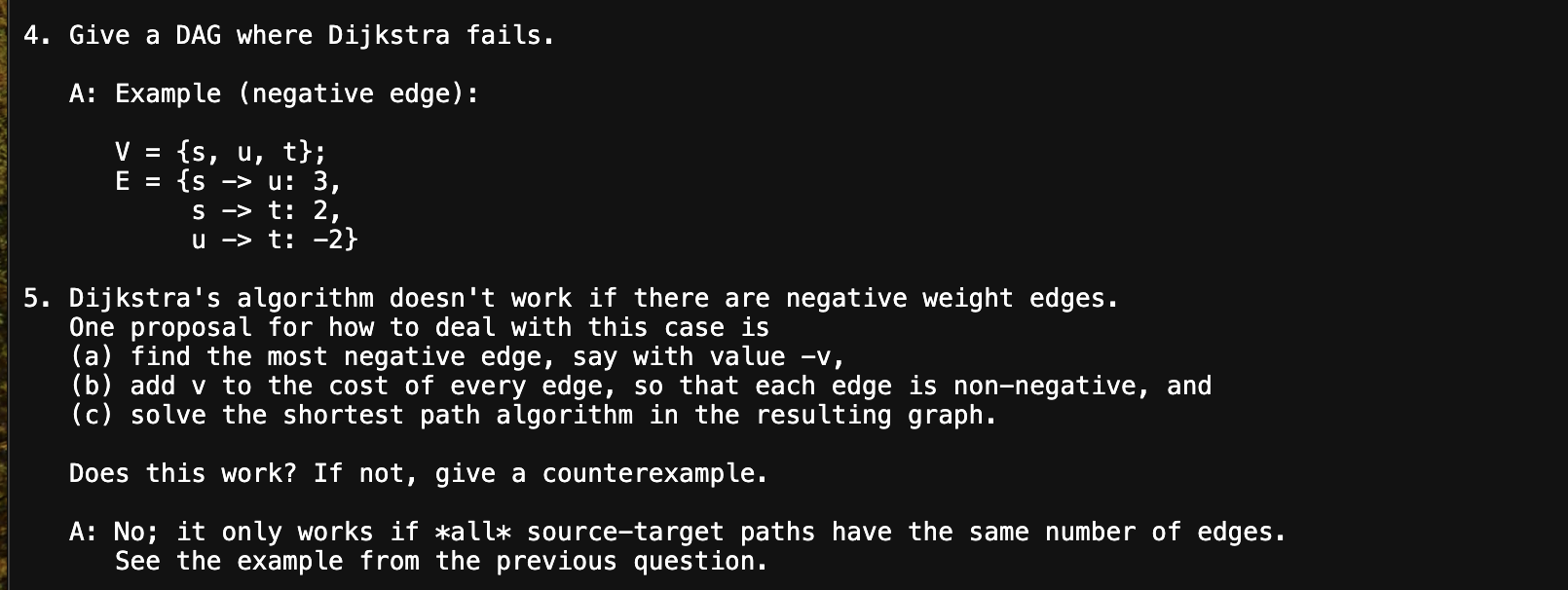
Give a DAG where Dijkstra fails.

A: Example $($negative edge$)$:

$v=\{s,u,t\}$;

$E=\{su$:$3,$

$st$:$2,$

$ut$:$-2\}$

Dijkstra's algorithm doesn't work if there are negative weight edges.

One proposal for how to deal with this case is

$($a$)$ find the most negative edge, say with value $-v,$

$($b$)$ add $v$ to the cost of every edge, so that each edge is non$-$negative, and

$($c$)$ solve the shortest path algorithm in the resulting graph.

Does this work? If not, give a counterexample.

A: No; it only works if source$-$target paths have the same number of edges.

See the example from the previous question.

Can you give me the example that this proposal works?

I dont quite understand what does it means it only works if $*$all$*$ source$-$target paths have the same number of edges.

Please also explain the order when the node get popped.