Give an algorithmn for this problem 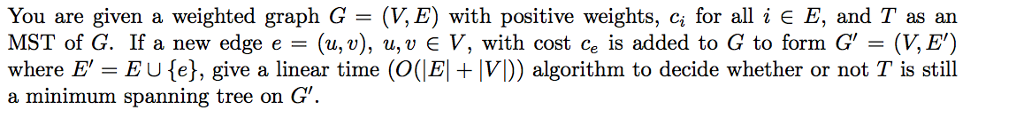You are given a weighted graph G=(V,E) with positive weights, c_i for all i in E, and T as an MST of G. If a new edge e=(u,v), u,v in V, with cost c_e is added to G to form G'=(V,E') where E' = E union {e}, give a linear time O(|E| + |V|) algorithm to decide whether or not T is still a minimum spanning tree on G'. (You can describe your algorithm in words; no pseudocode.)

You are given a weighted graph G = (V. E) with positive weights, ci for all i E, and T as an MST of G. If a new edge e = (u, v), u, v V, with cost ce ls added to G to form G' (V, E') where E, = EU {e), give a linear time (O(Bl+ |v|)) algorithm to decide whether or not T is still a minimum spanning tree on G