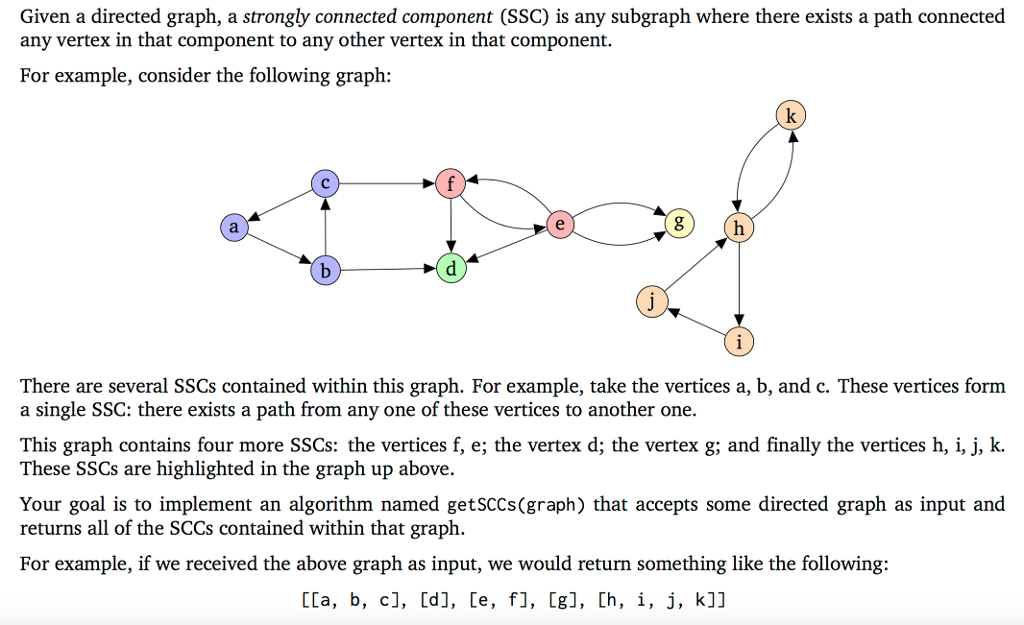
Given a directed graph, a strongly connected component (SSC) is any subgraph where there exists a path connected any vertex in that component to any other vertex in that component. For example, consider the following graph: There are several SSCs contained within this graph. For example, take the vertices a, b, and c. These vertices form a single SSC: there exists a path from any one of these vertices to another one. This graph contains four more SSCs: the vertices f, e; the vertex d; the vertex g; and finally the vertices h, i, j, k. These SSCs are highlighted in the graph up above. Your goal is to implement an algorithm named getsCCs(graph) that accepts some directed graph as input and returns all of the SCCs contained within that graph. For example, if we received the above graph as input, we would return something like the following: CCa, b, c], [d], le, fl, [g], Ch, i, j, k1] Given a directed graph, a strongly connected component (SSC) is any subgraph where there exists a path connected any vertex in that component to any other vertex in that component. For example, consider the following graph: There are several SSCs contained within this graph. For example, take the vertices a, b, and c. These vertices form a single SSC: there exists a path from any one of these vertices to another one. This graph contains four more SSCs: the vertices f, e; the vertex d; the vertex g; and finally the vertices h, i, j, k. These SSCs are highlighted in the graph up above. Your goal is to implement an algorithm named getsCCs(graph) that accepts some directed graph as input and returns all of the SCCs contained within that graph. For example, if we received the above graph as input, we would return something like the following: CCa, b, c], [d], le, fl, [g], Ch, i, j, k1]