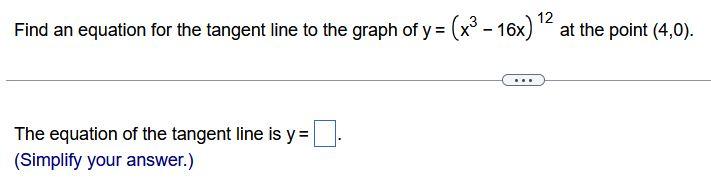
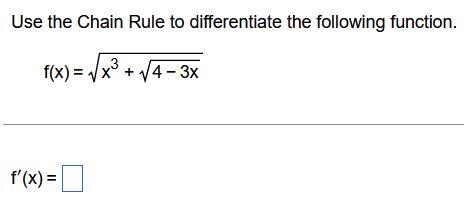
Given a total-revenue function R(x)=1000x20.3x and a total-cost function C(x)=1400(x2+3)3+900, both in thousands of dollars, find the rate at which total profit is changing when x items have been produced and sold. P(x)= When an object is dropped on a certain earth-like planet, the distance it falls in t seconds, assuming that air resistance is negligible, is given by s(t)=12t2 where s(t) is in feet. Suppose that a medic's reflex hammer is dropped from a hovering helicopter. Find (a) how far the hammer falls in 2sec, (b) how fast the hammer is traveling 2 sec after being dropped, and (c) the hammer's acceleration after it has been falling for 2 sec. Find an equation for the tangent line to the graph of y=(x316x)12 at the point (4,0). The equation of the tangent line is y= (Simplify your answer.) Use the Chain Rule to differentiate the following function. f(x)=x3+43x f(x)=