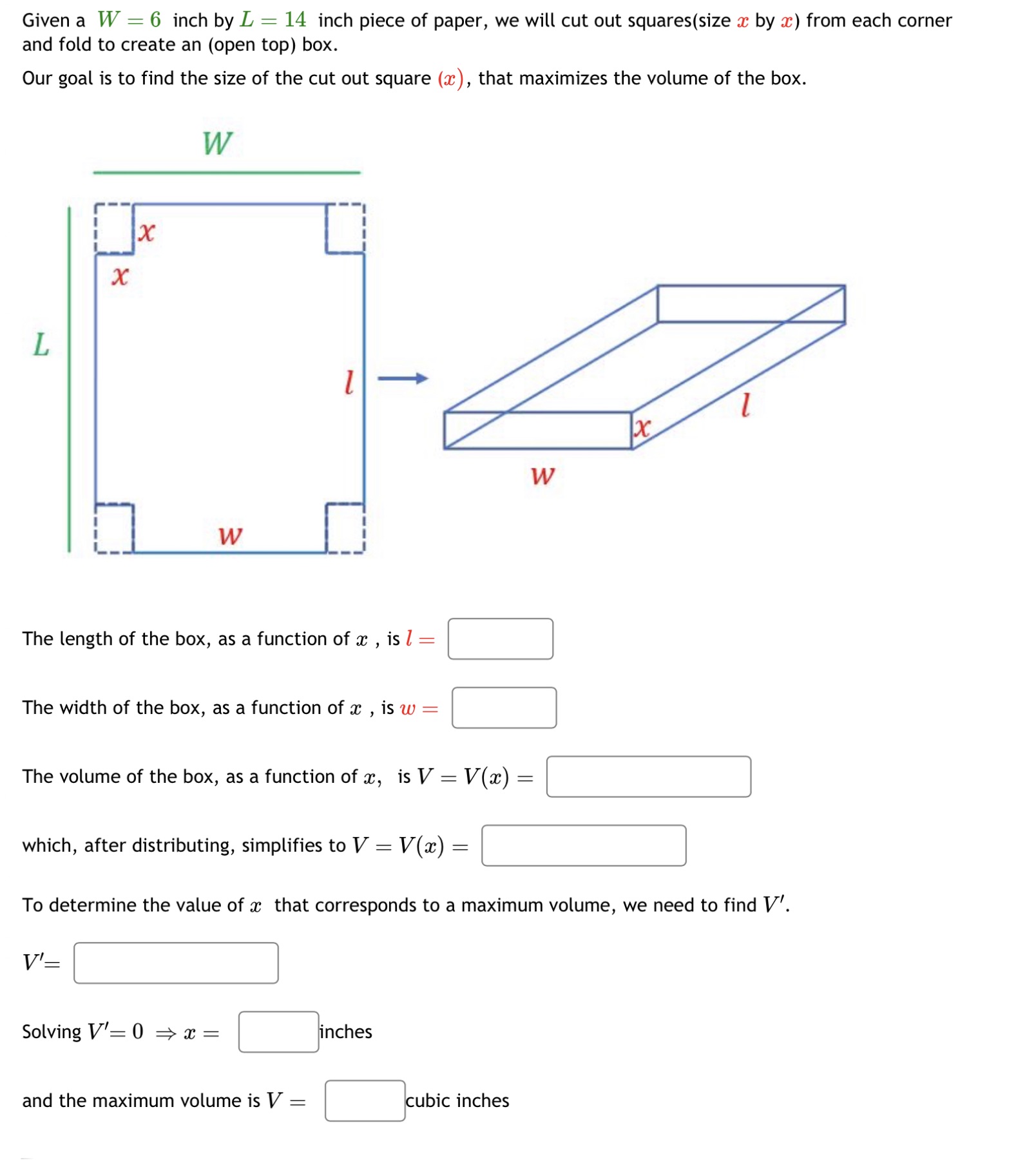
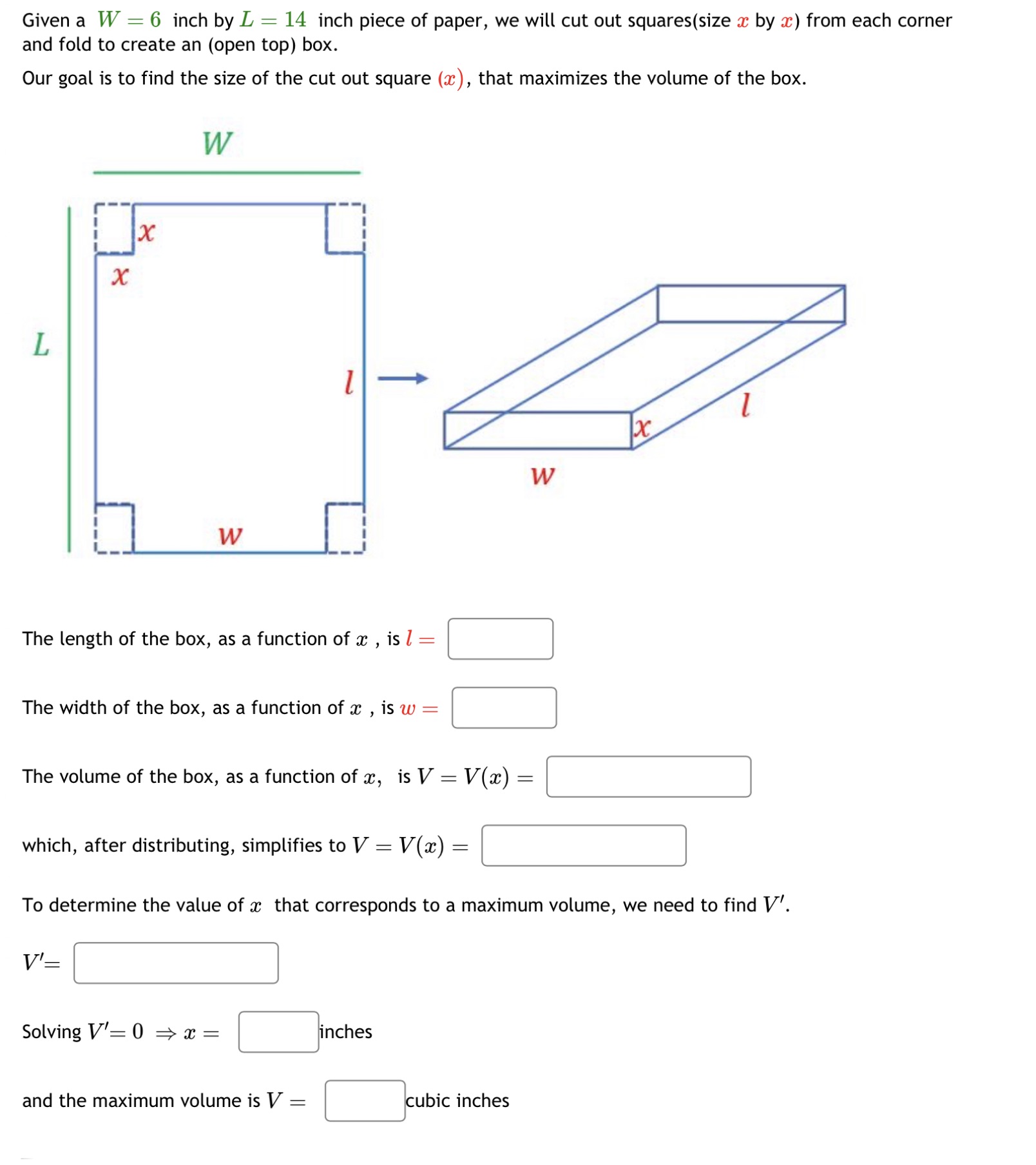
Given a W : 6 inch by L : 14 inch piece of paper, we will cut out squares(size m by at) from each corner and fold to create an (open top) box. Our goal is to find the size of the cut out square (m), that maximizes the volume of the box. The length of the box, as a function of a: , is l : [j The width of the box, as a function of a: , is w : [j The volume of the box, as a function of m, is V = V(:c) : :] which, after distributing, simplifies to V = V(:c) : :] To determine the value of a: that corresponds to a maximum volume, we need to find V'. V': :1 Solving V': 0 :> m : Sinches and the maximum volume is V : Subic inches