Question: Given a weighted connected graph G = (V, E) with m = |E| edges and n = |V | vertices where every edge e
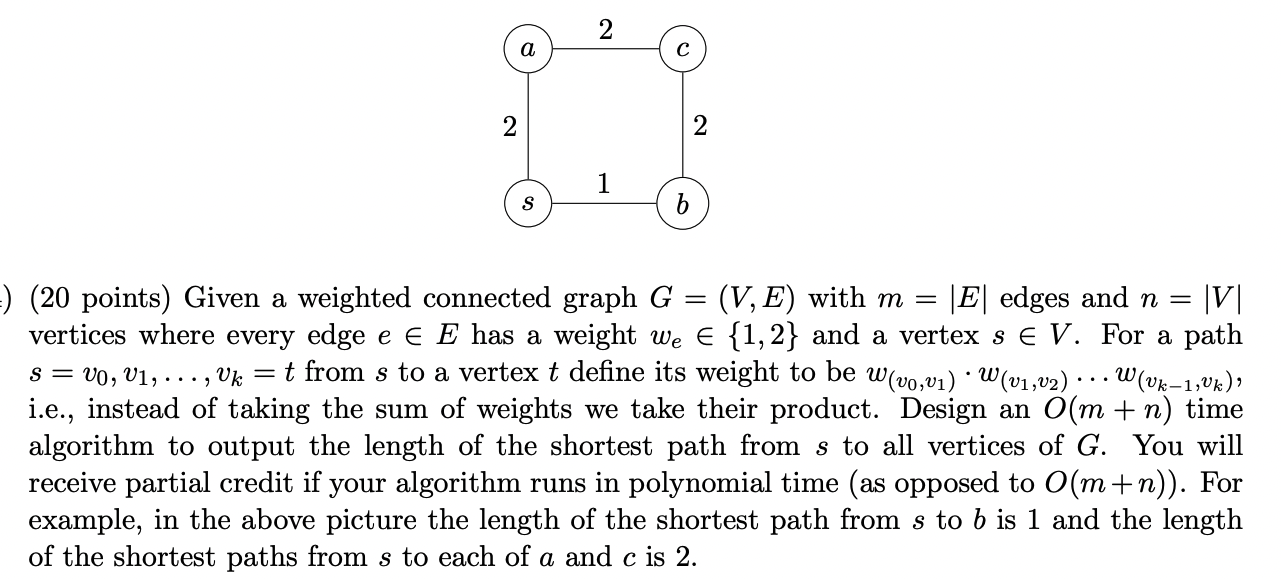
a 2 C 2 S 1 21 b :) (20 points) Given a weighted connected graph G = = (V,E) with m = |E| edges and n = |V| vertices where every edge e E has a weight we = {1,2} and a vertex s E V. For a path SVO, V1,..., Uk t from s to a vertex t define its weight to be w(v0, v) W(v1, v2) ... W (Vk-1, vk), i.e., instead of taking the sum of weights we take their product. Design an O(m + n) time algorithm to output the length of the shortest path from s to all vertices of G. You will receive partial credit if your algorithm runs in polynomial time (as opposed to O(m+n)). For example, in the above picture the length of the shortest path from s to b is 1 and the length of the shortest paths from s to each of a and c is 2.
Step by Step Solution
3.53 Rating (146 Votes )
There are 3 Steps involved in it
To find the length of the shortest path from vertex s to all other vertices in a weighted connected graph G we can use Dijkstras algorithm with slight modifications to handle the product of weights in... View full answer

Get step-by-step solutions from verified subject matter experts


