Given Below Find the head loss using the rose equation.

Each filter unit has a diameter of 30cm The average Porosity of all sand grains is 0.42 and the shape factor is 0.9. The total depth of filter bed is 5cm The water temperature is 10^oC

PLEASE IDENTIFY HOW YOU DETERMINE C_d AND V_A.

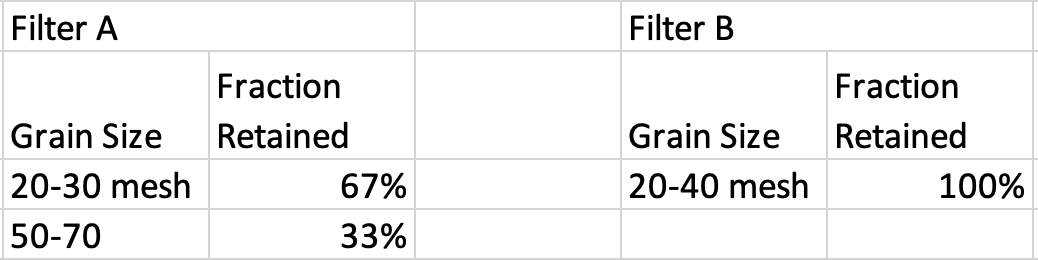
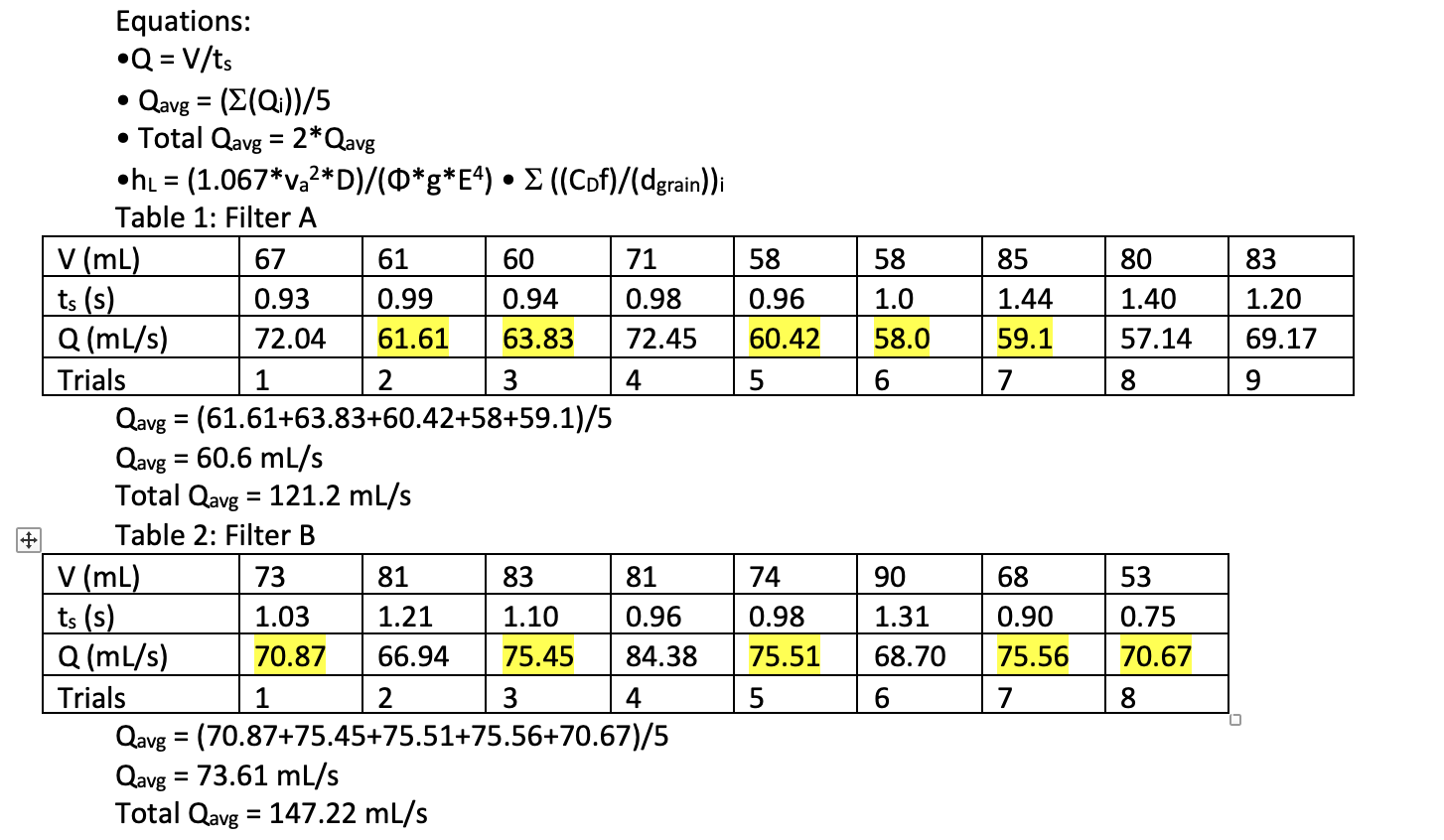
Filter A Filter B Grain Size 20-30 mesh 50-70 Fraction Retained 67% 33% Grain Size 20-40 mesh Fraction Retained 100% = 58 85 80 83 58 0.96 60.42 1.0 1.44 59.1 7 1.40 57.14 1.20 69.17 58.0 5 6 8 9 Equations: Q = V/ts Qavg = (E(Qi))/5 Total Qavg = 2* Qavg h = (1.067*va2*D)/(0*g*E4) E ((Cpf)/(dgrain)); Table 1: Filter A V (mL) 67 61 60 71 ts (s) 0.93 0.99 0.94 0.98 Q (ml/s) 72.04 61.61 63.83 72.45 Trials 2. 3 4 Qavg = (61.61+63.83+60.42+58+59.1)/5 Qavg = 60.6 ml/s Total Qavg = 121.2 ml/s Table 2: Filter B V(mL) 73 83 81 ts (s) 1.03 1.21 1.10 0.96 Q (ml/s) 70.87 66.94 75.45 84.38 Trials 1 2. 3 4 Qavg = (70.87+75.45+75.51+75.56+70.67)/5 Qavg = 73.61 mL/s Total Qavg = 147.22 ml/s = 81 74 0.98 75.51 5 90 1.31 68.70 68 0.90 75.56 7 53 0.75 70.67 6 8 = = . i=1 = 1.067 (v.) (D) " (Cp) (f) ? hi (0)(g)(e)4 d where hi frictional head loss through the filter, m a approach velocity, m/s D = depth of filter sand, m Cp = drag coefficient f = mass fraction of sand particles of diameter d d = diameter of sand grains, m = shape factor 8 acceleration due to gravity, m/s porosity = - = 2 = E =