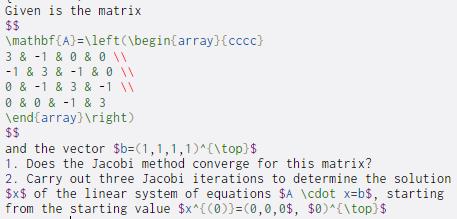
Given is the matrix $$ \mathbf{A}=\left(\begin{array}{cccc} 3 & 1 & 0 & 0 \\ -1 & 3 & -1 & 0 \\ 0&1 & 3 & -1 \\ 0 &0&1 & 3 \end{array} ight) $$ and the vector $b=(1,1,1,1)^{\top}$ 1. Does the Jacobi method converge for this matrix? 2. Carry out three Jacobi iterations to determine the solution $X$ of the linear system of equations $A \cdot x=b$, starting from the starting value $x^{(0))=(0,0,0$, $0)^{\top} $