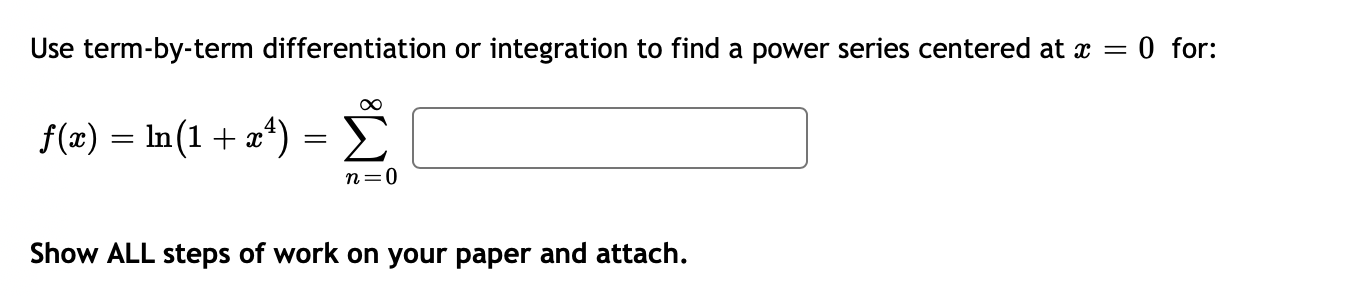
Given that x 3:\" with convergence in (1 , 1), find the power series for with center 0. _ 2 1 a: 0 173: 1 (X) n: 2 [:1 n=0 Identify its interval of convergence. The series is convergent from m = C] , left end included (enter Y or N): C] to a: = C] , right end included (enter Y or N): I:] Be sure to show all steps of work on your attached paper. Use tenn-by-term differentiation or integration to find a power series centered at a: = 0 for: 00 m=m= :2 :1 11:0 Show ALL steps of work on your paper and attach. Find the Taylor polynomial of degree 4 for the function an) = 1110:), centered at a = 5.9. (Leave your answer as the sums of powers of (a: (1).) W) = Be sure to show all steps of work on your paper. Using this polynomial, obtain this approximation: ln(6.2) m