Question: Given the following information: a) Using normal durations, compute the critical duration of the project. Identify the critical path(s). Calculate the normal direct project cost.
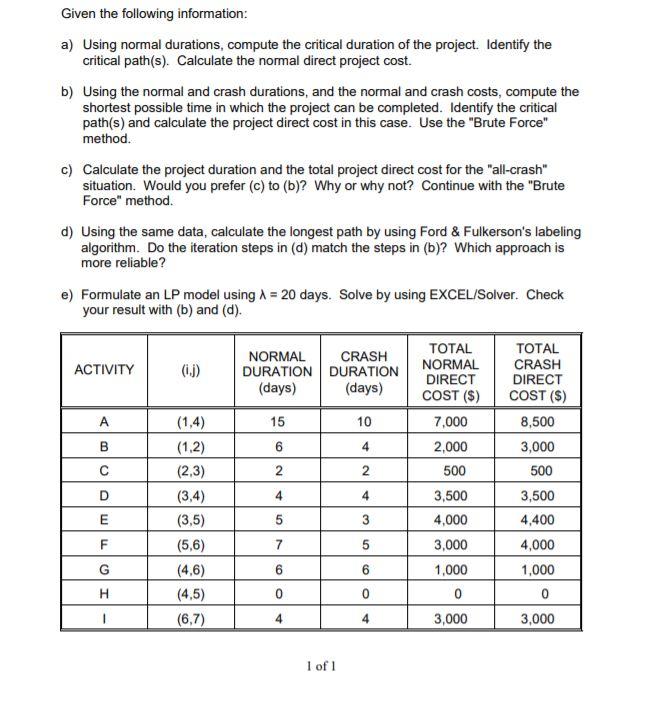
Given the following information: a) Using normal durations, compute the critical duration of the project. Identify the critical path(s). Calculate the normal direct project cost. b) Using the normal and crash durations, and the normal and crash costs, compute the shortest possible time in which the project can be completed. Identify the critical path(s) and calculate the project direct cost in this case. Use the "Brute Force" method. c) Calculate the project duration and the total project direct cost for the "all-crash" situation. Would you prefer (c) to (b)? Why or why not? Continue with the "Brute Force" method. d) Using the same data, calculate the longest path by using Ford & Fulkerson's labeling algorithm. Do the iteration steps in (d) match the steps in (b)? Which approach is more reliable? e) Formulate an LP model using A = 20 days. Solve by using EXCEL/Solver. Check your result with (b) and (d). ACTIVITY NORMAL CRASH DURATION DURATION (days) (days) TOTAL CRASH DIRECT COST ($) 8,500 3,000 500 A 15 10 B 6 4 C 2 2 TOTAL NORMAL DIRECT COST ($) 7,000 2,000 500 3,500 4,000 3,000 1,000 0 D 4 4 (1.4) (1,2) (2,3) (3,4) (3,5) (5,6) (4,6) (4,5) (6,7) E 5 3 F 7 5 6 3,500 4,400 4,000 1,000 0 3,000 G 6 H 0 0 4 4 3,000 1 of 1 Given the following information: a) Using normal durations, compute the critical duration of the project. Identify the critical path(s). Calculate the normal direct project cost. b) Using the normal and crash durations, and the normal and crash costs, compute the shortest possible time in which the project can be completed. Identify the critical path(s) and calculate the project direct cost in this case. Use the "Brute Force" method. c) Calculate the project duration and the total project direct cost for the "all-crash" situation. Would you prefer (c) to (b)? Why or why not? Continue with the "Brute Force" method. d) Using the same data, calculate the longest path by using Ford & Fulkerson's labeling algorithm. Do the iteration steps in (d) match the steps in (b)? Which approach is more reliable? e) Formulate an LP model using A = 20 days. Solve by using EXCEL/Solver. Check your result with (b) and (d). ACTIVITY NORMAL CRASH DURATION DURATION (days) (days) TOTAL CRASH DIRECT COST ($) 8,500 3,000 500 A 15 10 B 6 4 C 2 2 TOTAL NORMAL DIRECT COST ($) 7,000 2,000 500 3,500 4,000 3,000 1,000 0 D 4 4 (1.4) (1,2) (2,3) (3,4) (3,5) (5,6) (4,6) (4,5) (6,7) E 5 3 F 7 5 6 3,500 4,400 4,000 1,000 0 3,000 G 6 H 0 0 4 4 3,000 1 of 1





