Given the steady$-$state, non$-$dimensional velocity field:

vec$(V)(x,y)=cscx(i)+\frac{1}{2}y(j)$ over the domain $0x\frac{}{2}$ and $0y{2}^2$

$[2$pts$]($a$)$ Compute the equation of the streamlines $($i$.$e$.,$ family of curves$)$ for this flow

field. Leave your answer in the form of a graph: $g(x,y)=0.$ Warning: Do not attempt

to find a functional form: $y=f(x),$ or $x=h(y),$ at this stage in the problem.

$[2$pts$]($b$)$ Determine the equation for the streamline going through the point $(0,1)$ in the

form of a function: $y=f(x).$

$[2$pts$]($c$)$ Compute the pathline for a particle that is moving with the velocity field start$-$

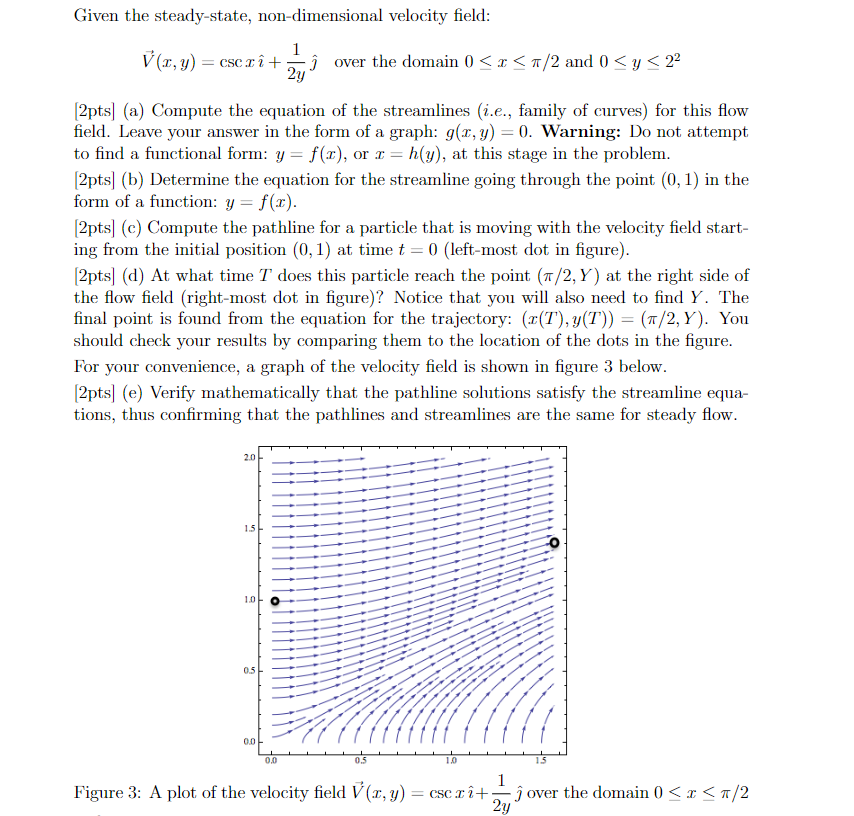
ing from the initial position $(0,1)$ at time $t=0($left$-$most dot in figure$).$

$[2$pts$]($d$)$ At what time $T$ does this particle reach the point $(\frac{}{2},Y)$ at the right side of

the flow field $($right$-$most dot in figure$)?$ Notice that you will also need to find $Y.$ The

final point is found from the equation for the trajectory: $(x(T),y(T))=(\frac{}{2},Y).$ You

should check your results by comparing them to the location of the dots in the figure.

For your convenience, a graph of the velocity field is shown in figure $3$ below.

$[2$pts$]($e$)$ Verify mathematically that the pathline solutions satisfy the streamline equa$-$

tions, thus confirming that the pathlines and streamlines are the same for steady flow.

Figure $3$: A plot of the velocity field vec$(V)(x,y)=cscx(i)+\frac{1}{2}y(j)$ over the domain $0x\frac{}{2}$