Converging duct flow is modeled by the steady, two- dimensional velocity field of Prob. 4–17. The pressure field is given by

where P₀ is the pressure at x = 0. Generate an expression for the rate of change of pressure following a fluid particle.

Data from Problem 17

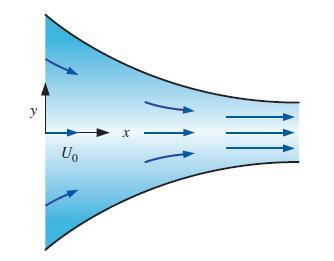
Consider steady, incompressible, two-dimensional flow through a converging duct (Fig. P4–17). A simple approximate velocity field for this flow is

where U₀ is the horizontal speed at x = 0. Note that this equation ignores viscous effects along the walls but is a reasonable approximation throughout the majority of the flow field. Calculate the material acceleration for fluid particles passing through this duct. Give your answer in two ways:

(1) As acceleration components a_x and a_y 

(2) As acceleration vector a(vector)

P = Po -[20,x+ 2U bx + b(x + y) - 1-)]