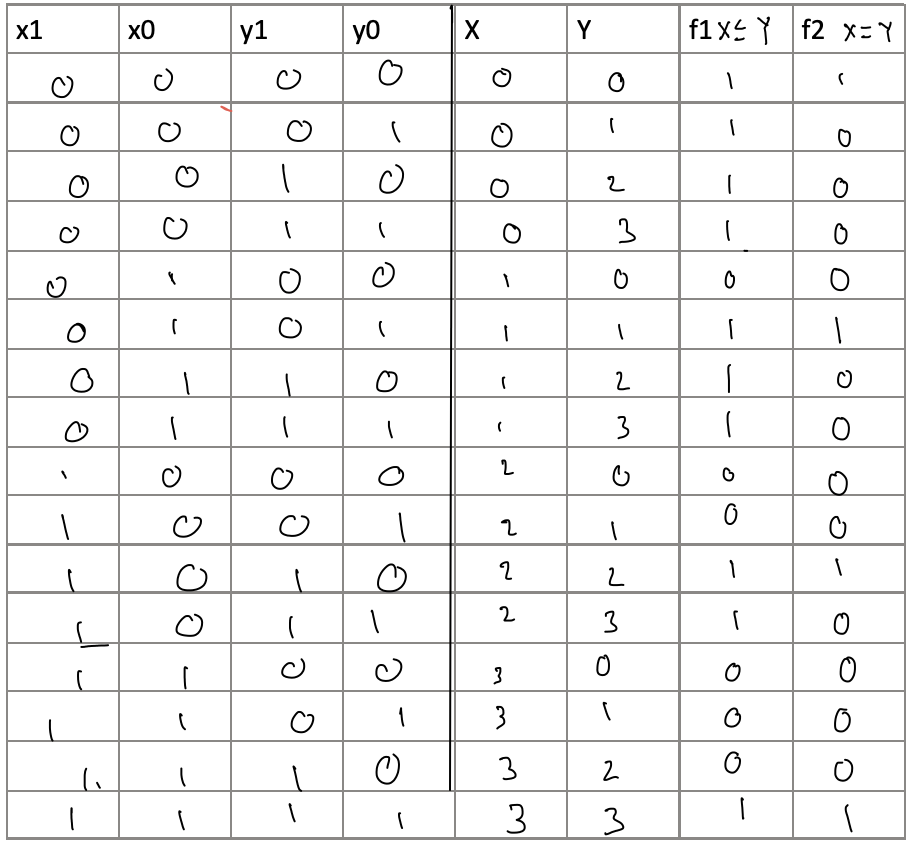
Given the table below, derive a boolean expression in canonical PRODUCT$-$OF$-$SUMS form for each function f$1$ and f$2.$ Use algebraic manipulation to simplify the Boolean expression for f$1($leave in minimal product$-$of$-$sum form$).$ SHOW all your steps and how you got to the final answer. For f$2,$ we'll let Quartus do the work for us$.$ Enter the Boolean expression $($canonical for f$2)$ into Quartus in $2$ different ways.$\backslash$table$[[$x $1,$x $0,$y $1,$y $0,$x$,$y$,$f$1$xy$,$f$2$x$=$y$],[0,0,0,0,0,0,1,1],[0,0,0,1,0,1,1,0],[0,0,1,0,0,2,1,0],[0,0,1,1,0,3,1,0],[0,1,0,0,1,0,0,0],[0,1,0,1,1,1,1,1],[0,1,1,0,1,2,1,0],[0,1,1,1,1,3,1,0],[1,0,0,0,2,0,0,0],[1,0,0,1,2,1,0,0],[1,0,1,0,2,2,1,1],[1,0,1,1,2,3,1,0],[1,1,0,0,3,0,0,0],[1,1,0,1,3,1,0,0],[1,1,1,0,3,2,0,0],[1,1,1,1,3,3,1,1]]\backslash$table$[[$x$1,$x$0,$y$1,$y$0,$X$,$Y$,$f$1$ xy$,$f$2$ x$=$y$],[0,0,0,0,0,0,1,1],[0,0,0,1,0,1,1,0],[0,0,1,0,0,2,1,0],[0,0,1,1,0,3,1,0],[0,1,0,0,1,0,0,0],[0,1,0,1,1,1,1,1],[0,1,1,0,1,2,1,0],[0,1,1,1,1,3,1,0],[1,0,0,0,2,0,0,0],[1,0,0,1,2,1,0,0],[1,0,1,0,2,2,1,1],[1,0,1,1,2,3,1,0],[1,1,0,0,3,0,0,0],[1,1,0,1,3,1,0,0],[1,1,1,0,3,2,0,0],[1,1,1,1,3,3,1,1]]$