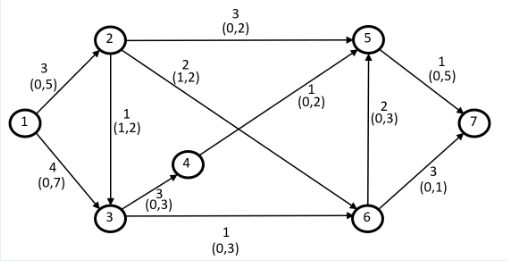
Given this problem of minimum$-$cost flow problem in the picture: the source is node $1$ and the sink is node $7.$ The flow quantity needed to transport from node $1$ to node $7$ is $4.$ For each arc we have:

$-$ The cost of of the arc.

$-$ A interval $($lower bound, upper bound$)$ is the minimum and maximum capacity flow transited on each arc.

For each arc $($i$,$j$),$ x$\_$ij is the decision variable representing the flow transported on that arc.

Select all the right options:

a$.$ x$\_12=3,$ x$\_13=1,$ x$\_23=1,$ x$\_25=1,$ x$\_26=1,$ x$\_34=0,$ x$\_36=2,$ x$\_45=0,$ x$\_57=4,$ x$\_65=3,$ x$\_67=0$ is a feasible solution

b$.$ x$\_12=2,$ x$\_13=3,$ x$\_23=1,$ x$\_25=0,$ x$\_26=1,$ x$\_34=0,$ x$\_36=3,$ x$\_45=0,$ x$\_57=3,$ x$\_65=3,$ x$\_67=1$ is a feasible solution

c$.$The optimal value for the solution x$\_12=2,$ x$\_13=2,$ x$\_23=1,$ x$\_25=0,$ x$\_26=1,$ x$\_34=2,$ x$\_36=1,$ x$\_45=2,$ x$\_57=3,$ x$\_65=1,$ x$\_67=1$ is $34$

d$.$The optimal value for the solution x$\_12=2,$ x$\_13=2,$ x$\_23=1,$ x$\_25=0,$ x$\_26=1,$ x$\_34=2,$ x$\_36=1,$ x$\_45=2,$ x$\_57=3,$ x$\_65=1,$ x$\_67=1$ est $4.$