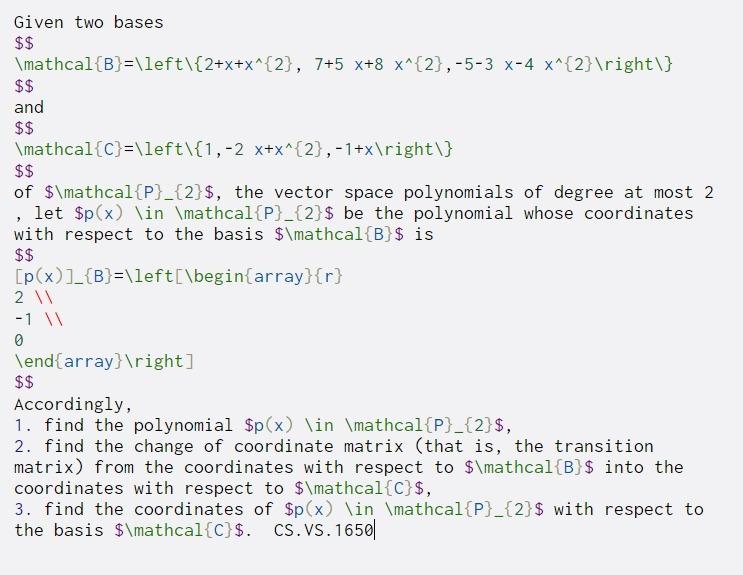
Given two bases $$ \mathcal{B}=\left\{2+x+x^{2}, 7+5 x+8 X^{2}, -5-3 X-4 X^{2} ight\} $$ and $$ \mathcal{C}=\left\{1,-2 x+x^{2},-1+x ight\} $$ of $\mathcal{P}_{2}$, the vector space polynomials of degree at most 2 , let $p(x) \in \mathcal{P}_{2}$ be the polynomial whose coordinates with respect to the basis $\mathcal{B}$ is $$ [p(x)}{B}=\left\begin{array}{r} 2 -1 1 0 \end{array} ight] $$ Accordingly, 1. find the polynomial $p(x) \in \mathcal{P}_{2}$, 2. find the change of coordinate matrix (that is, the transition matrix) from the coordinates with respect to $\mathcal{B}$ into the coordinates with respect to $\mathcal{C}$, 3. find the coordinates of $p(x) \in \mathcal{P}_{2}$ with respect to the basis $\mathcal{C}$. CS.VS. 1650