glBegin(int mode); and glEnd( void );

glBegin and glEnd delimit the vertices of a primitive or a group of like primitives. What this means is that everytime you want to draw a primitive on the screen you will first have to call glBegin, specifying what kind of primitive it is that you want to draw in the mode parameter of glBegin, and then list all vertices one by one (by sequentially calling glVertex) and finally call glEnd to let OpenGL know that you're done drawing a primitive. The parameter mode of the function glBegin can be one of the following:

GL_POINTS

GL_LINES

GL_LINE_STRIP

GL_LINE_LOOP

GL_TRIANGLES

GL_TRIANGLE_STRIP

GL_TRIANGLE_FAN

GL_QUADS

GL_QUAD_STRIP

GL_POLYGON

These flags are self-explanatory. As an example I want to show how to draw some primitives and then you will be able to understand how to draw the rest of them.

// this code will draw a point located at [100, 100, -25]

glBegin(GL_POINTS);

glVertex3f(100.0f, 100.0f, -25.0f);

glEnd( );

// next code will draw a line at starting and ending coordinates specified by glVertex3f

glBegin(GL_LINES);

glVertex3f(100.0f, 100.0f, 0.0f);// origin of the line

glVertex3f(200.0f, 140.0f, 5.0f); // ending point of the line

glEnd( );

// the following code draws a triangle

glBegin(GL_TRIANGLES);

glVertex3f(100.0f, 100.0f, 0.0f);

glVertex3f(150.0f, 100.0f, 0.0f);

glVertex3f(125.0f, 50.0f, 0.0f);

glEnd( );

// this code will draw two lines "at a time" to save

// the time it takes to call glBegin and glEnd.

glBegin(GL_LINES);

glVertex3f(100.0f, 100.0f, 0.0f);// origin of the FIRST line

glVertex3f(200.0f, 140.0f, 5.0f); // ending point of the FIRST line

glVertex3f(120.0f, 170.0f, 10.0f); // origin of the SECOND line

glVertex3f(240.0f, 120.0f, 5.0f); // ending point of the SECOND line

glEnd( );

This functionality can be used with any primitive as long as you specify the right number of vertices. For example, to draw two lines in one glBegin-glEnd sequence you need to specify FOUR vertices. Likewise, to draw 2 triangles in one shot, you would call glBegin(GL_TRIANGLES) and specify SIX vertices afterwards. glBegin and glEnd can be expensive calls in tight loops.

If you have an object containing a polygon and, say a line (to indicate its normal?), it would be better to have two loops: first one for drawing all the polygons in the object and second one to draw all the lines in the objects, rather than calling glBegin and glEnd 4 times in one loop each iteration.

glVertex is not constrained to be the only function you can use inside glBegin and glEnd. Here is the full listing of all functions you can use inside glBegin and glEnd

glVertex

glColor

glIndex

glNormal

glTexCoord

glEvalCoord

glEvalPoint

glMaterial

glEdgeFlag

If any other OpenGL function is called between glBegin and glEnd, the error flag is set and the function is ignored.

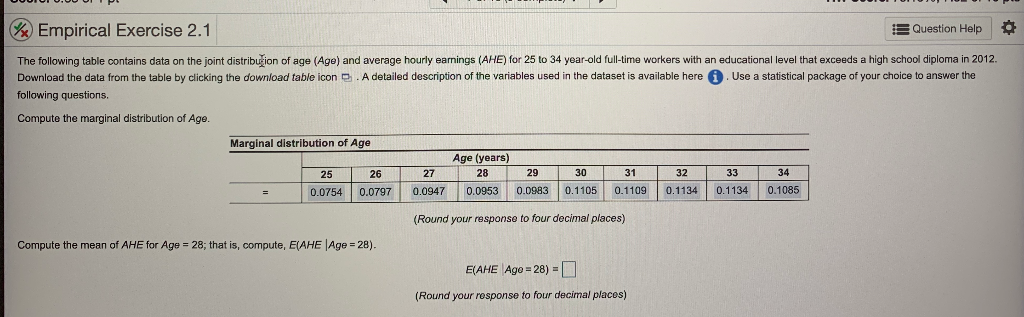
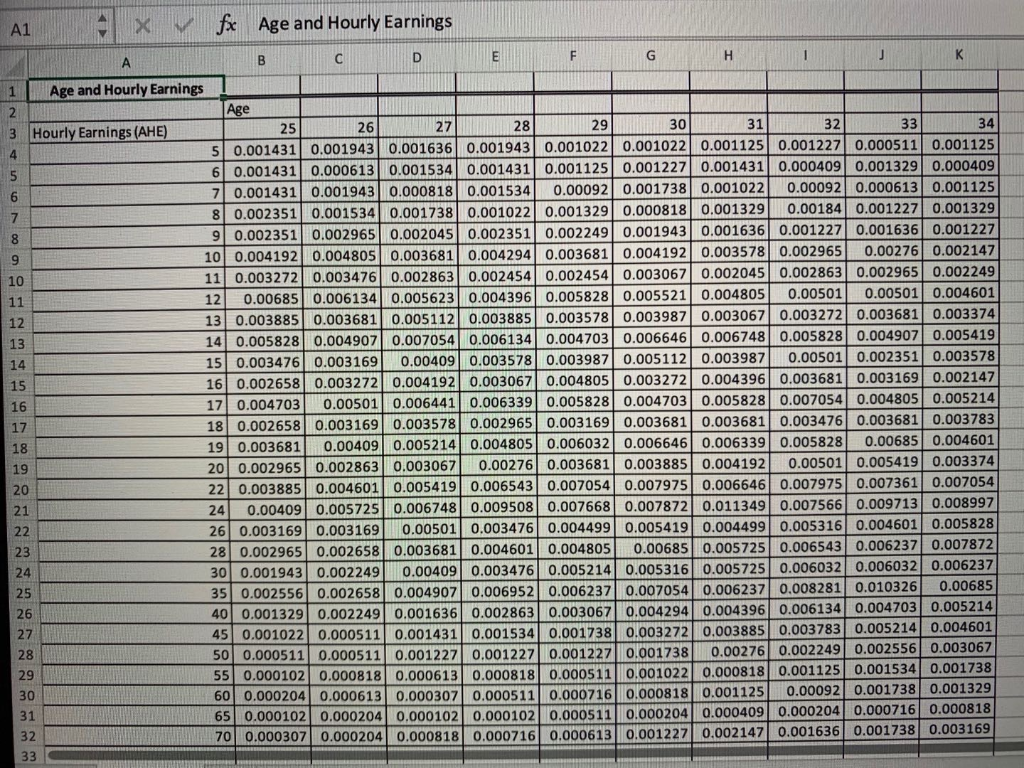
Empirical Exercise 2.1 Question Help The following table contains data on the joint distribution of age (Age) and average hourly earnings (AHE) for 25 to 34 year-old full-time workers with an educational level that exceeds a high school diploma in 2012. Download the data from the table by clicking the download table icon @ . A detailed description of the variables used in the dataset is available here (1) . Use a statistical package of your choice to answer the following questions. Compute the marginal distribution of Age. Marginal distribution of Age Age (years) 25 26 27 28 29 30 31 32 33 34 0.0754 0.0797 0.0947 0.0953 0.0983 0.1105 0.1109 0.1134 0.1134 0.1085 (Round your response to four decimal places) Compute the mean of AHE for Age = 28; that is, compute, E(AHE | Age = 28). E(AHE Ago = 28) = (Round your response to four decimal places)A1 x fx Age and Hourly Earnings B C D E G H K 1 Age and Hourly Earnings Age W N Hourly Earnings (AHE) 25 26 27 28 29 30 31 32 33 34 5 0.001431 0.001943 0.001636 0.001943 0.001022 0.001022 0.001125 0.0012270 0.000511 0.001125 6 0.001431 0.000613 0.001534 0.001431 0.001125 0.001227 0.001431 0.000409 0.001329 0.000409 7 0.001431 0.001943 0.000818 0.001534 0.00092 0.001738 0.001022 0.00092 0.000613 0.001125 8 0.002351 0.001534 0.001738 0.001022 0.001329 0.000818 0.001329 0.00184 0.001227 0.001329 9 0.002351 0.002965 0.002045 0.002351 0.002249 0.001943 0.001636 0.001227 0.001636 0.001227 10 0.004192 0.004805 0.003681 0.004294 0.003681 0.004192 0.003578 0.002965 0.00276 0.002147 11 0.003272 0.003476 0.002863 0.002454 0.002454 0.003067 0.002045 0.002863 0.002965 0.002249 11 12 0.00685 0.006134 0.005623 0.004396 0.005828 0.005521 0.004805 0.00501 0.00501 0.004601 12 13 0.003885 0.003681 0.005112 0.003885 0.003578 0.003987 0.003067 0.003272 0.003681 0.003374 14 0.005828 0.004907 0.007054 0.006134 0.004703 0.006646 0.006748 0.005828 0.004907 0.005419 15 0.003476 0.003169 0.00409 0.003578 0.003987 0.005112 0.003987 0.00501 0.002351 0.003578 16 0.002658 0.003272 0.004192 0.003067 0.004805 0.003272 0.004396 0.003681 0.003169 0.002147 17 0.004703 0.00501 0.006441 0.006339 0.005828 0.004703 0.005828 0.007054 0.004805 0.005214 18 0.002658 0.003169 0.003578 0.002965 0.003169 0.003681 0.003681 0.003476 0.003681 0.003783 19 0.003681 0.00409 0.005214 0.004805 0.006032 0.006646 0.006339 0.005828 0.00685 0.004601 19 20 0.002965 0.002863 0.003067 0.00276 0.003681 0.003885 0.004192 0.00501 0.005419 0.003374 20 22 0.003885 0.004601 0.005419 0.006543 0.007054 0.007975 0.006646 0.007975 0.007361 0.007054 21 24 0.00409 0.005725 0.006748 0.009508 0.007668 0.007872 0.011349 0.007566 0.009713 0.008997 22 26 0.003169 0.003169 0.00501 0.003476 0.004499 0.005419 0.004499 0.005316 0.004601 0.005828 23 28 0.002965 0.002658 0.003681 0.004601 0.004805 0.00685 0.005725 0.006543 0.006237 0.007872 24 30 0.001943 0.002249 0.00409 0.003476 0.005214 0.005316 0.005725 0.006032 0.006032 0.006237 25 35 0.002556 0.002658 0.004907 0.006952 0.006237 0.007054 0.006237 0.008281 0.010326 0.00685 26 40 0.001329 0.002249 0.001636 0.002863 0.003067 0.004294 0.004396 0.006134 0.004703 0.005214 IN 45 0.001022 0.000511 0.001431 0.001534 0.001738 0.003272 0.003885 0.003783 0.005214 0.004601 28 50 0.000511 0.000511 0.001227 0.001227 0.001227 0.001738 0.00276 0.002249 0.002556 0.003067 29 55 0.000102 0.000818 0.000613 0.000818 0.000511 0.001022 0.000818 0.001125 0.001534 0.001738 30 60 0.000204 0.000613 0.000307 0.000511 0.000716 0.000818 0.001125 0.00092 0.001738 0.001329 31 65 0.000102 0.000204 0.000102 0.000102 0.000511 0.000204 0.000409 0.000204 0.000716 0.000818 32 70 0.000307 0.000204 0.000818 0.000716 0.000613 0.001227 0.002147 0.001636 0.001738 0.003169 33