Goal:

Implement Google's page rank using C++.

Input

Line 1 contains the number of lines (n) that will follow and the number of power iterations you need to perform. Each line from 2 to n will contain two URLs from_page to_page separated by a space. This means from_page points to the URL to_page.

*the first power iteration is simply the starting point for page ranks*

*2 power iterations means one matrix multiplication*

*3 power iterations means two matrix multiplications*

Output

Print the PageRank of all pages after n powerIterations in ascending alphabetical order of webpage. Also, round off the rank of the page to two decimal places.

Google Page Rank

In late 90s as the number of webpages on the internet were growing exponentially different search engines were trying different approaches to rank the webpages. At Stanford, two computer science PhD students, Sergey Brin and Larry Page were working on the following questions: How can we trust information? Why are some web pages more important than others? Their research led to the formation of the Google search engine. In this programming assignment, you are required to implement a simplified version of the original PageRank algorithm on which Google was built.

Representing the Web as a Graph

The idea that the entire internet can be represented as a graph. Each node represents a webpage and each edge represents a link between two webpages. This graph can be implemented as an Adjacency Matrix or an Adjacency List.

We are explaining the assignment in the form of an Adjacency Matrix. We represent the graph in the form of |V|x|V| matrix where |V| is the total number of vertices in the graph. A vertex represents a webpage in the internet. Thus, if there is an edge from Vi to Vj page i points to page j. In the adjacency matrix Mji>0 if there is an edge and 0 otherwise. Note that this is flipped compared to the adjacency matrix format we studied.

Core Ideas of PageRank

1. Important web pages will point to other important webpages.

2. Each page will have a score and the results of the search will be based on the page score (called page rank).

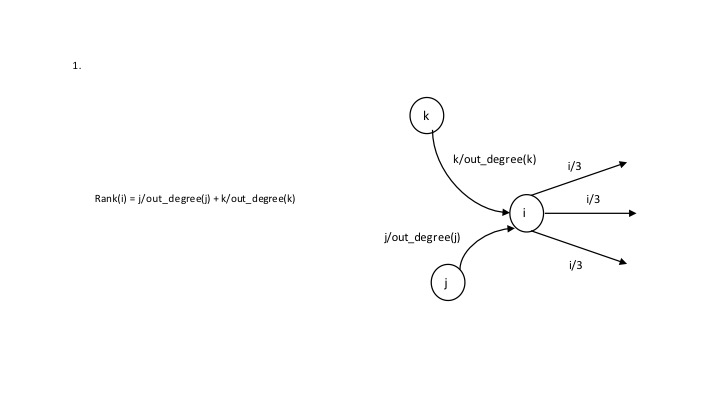
Each webpage is thus a node in the directed graph and has incoming edges and outgoing edges. Each node has a rank. According to PageRank, this rank is equally split among the nodes outgoing links and this rank is equal to the sum of the incoming ranks. The rank is based on the indegree (the number of nodes pointing to it) and the importance of incoming node. This is important considering lets say you create your personal website and have a million links to other pages of importance. If this was not the case and rank used out links, we can easily dupe the algorithm. Therefore, the rank is based on in-links.

Sample Problem

Input:

7 2

google.com mail.com

google.com maps.com

facebook.com ufl.edu

ufl.edu google.com

ufl.edu mail.com

maps.com facebook.com

mail.com maps.com

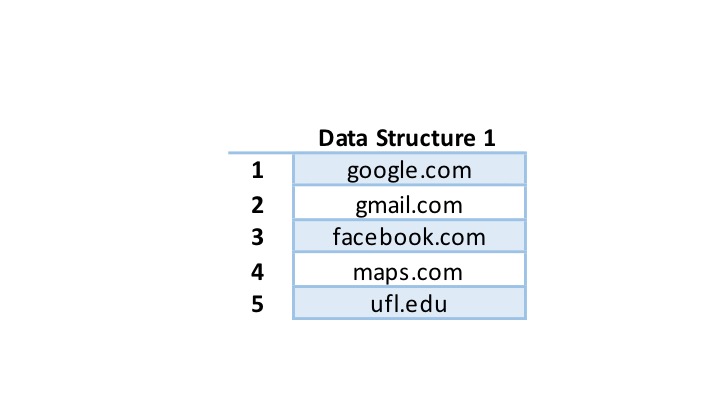
Step 1: Map URLs to a unique ID

1 google.com

2 mail.com

3 facebook.com

4 maps.com

5 ufl.edu

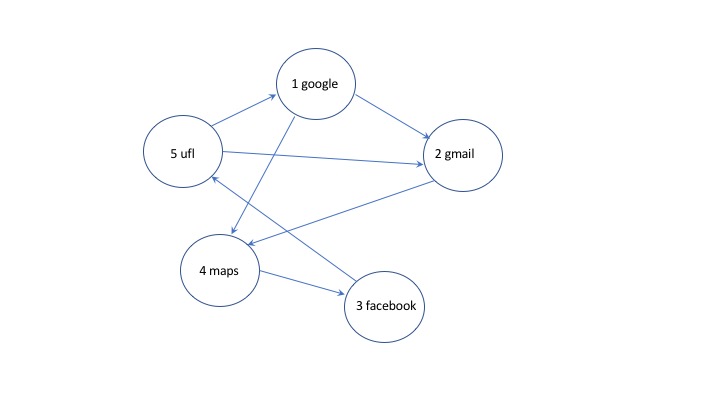
Step 2. Graph Representation

Here is the graph for our example:

The initial values Mji in the adjacency matrix are 1/di where di is the outdegree of vertex i.

For our graph, the adjacency matrix will look like:

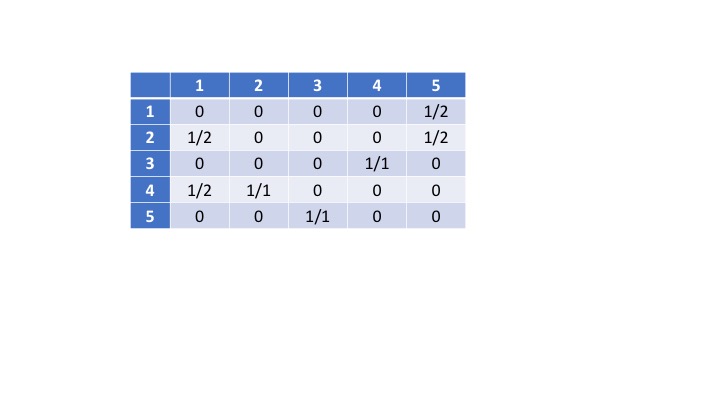
"5 UFL" points to "1 google". 5 has outdegree 2, so sends 1/2 its pagerank to 1. So M15 = 1/2.

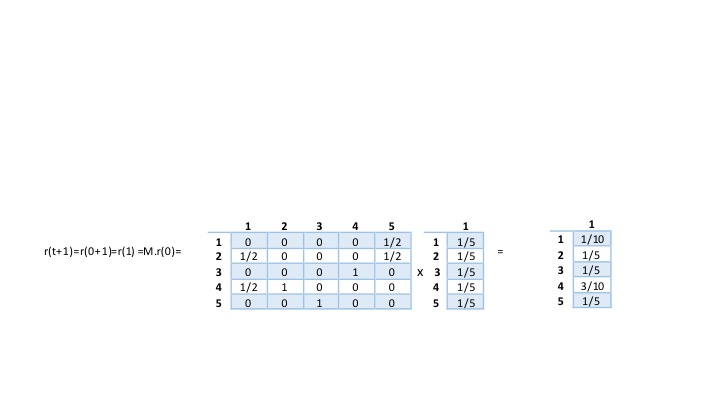
Step 3: Power Iteration r(t+1) = M*r(t)

This means that a rank of the webpage at time t+1 is equal to the rank of that page at time t multiplied by matrix, M. To achieve this, we create our matrix M based on input. Next, we initialize r(t) which is a matrix of size |V|x1 and consists of the ranks of every webpage. We initialize r(t) to 1/|V|. Next we compute power_iterations based on our input.

Yout degreelk)S /3 Ranki)j/out degreej) k/out degree(k) i/3 i/out_degreeli) i/3 Yout degreelk)S /3 Ranki)j/out degreej) k/out degree(k) i/3 i/out_degreeli) i/3