Question: Good Afternoon Can I get help with this task? I would greatly appreciate it. If you know how to help then please help me. However,
Good Afternoon
Can I get help with this task? I would greatly appreciate it. If you know how to help then please help me. However, if you don't know how to help me. Then let another tutor try and thanks for trying to help me.


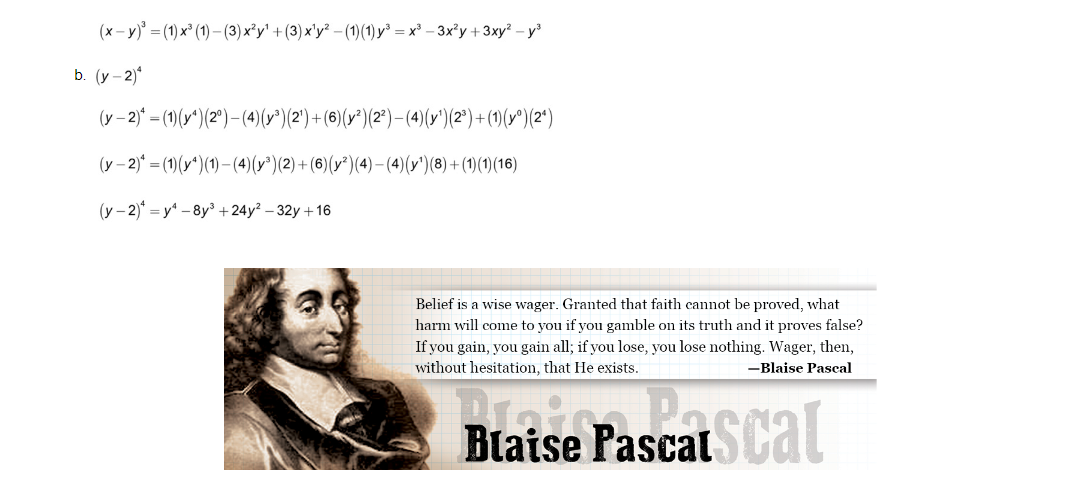

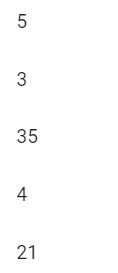

![after a devout French mathematician Blaise [blez] Pascal. Pascal's Triangle 1 Row](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2024/10/6703ebc0e1817_2086703ebc0c9888.jpg)

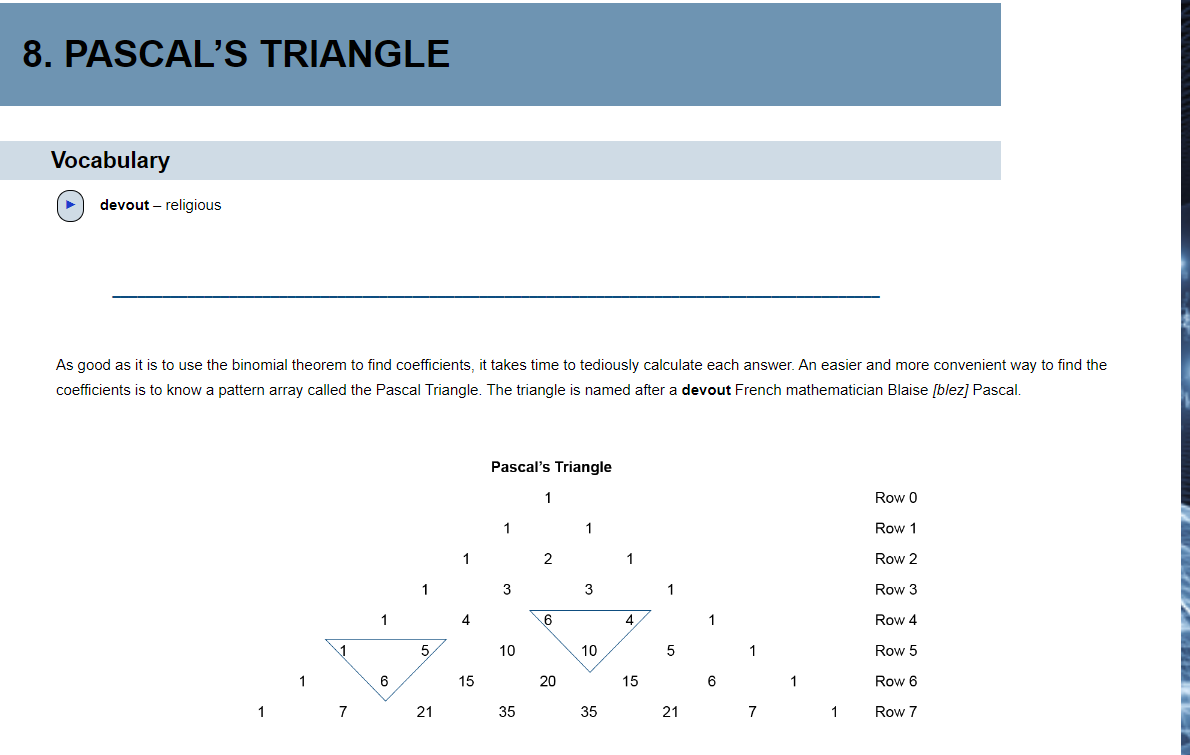
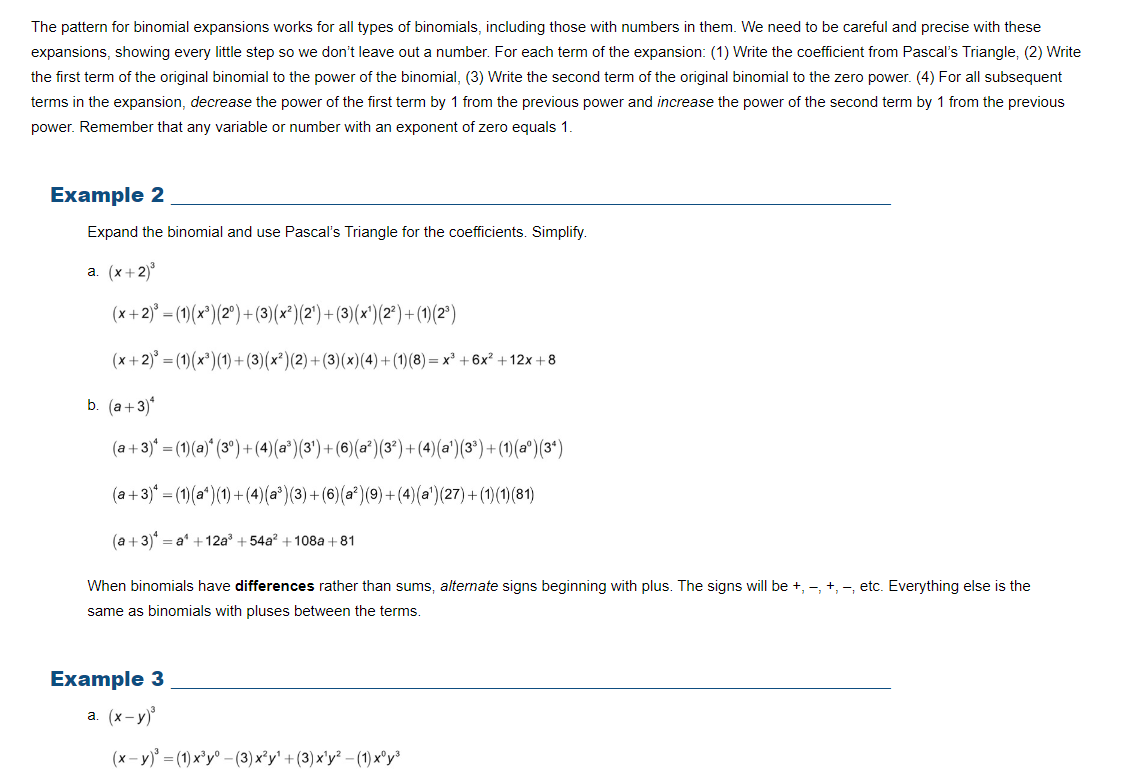
8. PASCAL'S TRIANGLE Vocabulary devout - religious As good as it is to use the binomial theorem to find coefficients, it takes time to tediously calculate each answer. An easier and more convenient way to find the coefficients is to know a pattern array called the Pascal Triangle. The triangle is named after a devout French mathematician Blaise [blez] Pascal. Pascal's Triangle 1 Row 0 1 Row 1 2 Row 2 7 3 3 Row 3 6 A Row 4 5 10 10 5 Row 5 15 20 15 6 Row 6 1 7 21 35 35 21 7 1 Row 7The top row with a "1" is referred to as Row 0 so that the numbers in a particular row will match the corresponding exponent in a binomial. For example, the numbers in Row 2 are the coefficients for the terms in the binomial (x + y)". Just as the coefficient for each end term in a binomial expansion is 1, the number at the ends of each row in the Triangle is 1. Notice, as Pascal did and as shown within the superimposed triangles, that a number in a row is the sum of the two numbers on each side and in the row above it. Now, instead of using the binomial theorem, we can simply look at Pascal's Triangle and easily find the coefficient for all the corresponding terms in a binomial expansion. To develop a new row, write the number 1 on each end and then use the triangle method to find the new numbers by adding the two numbers immediately above each one. In faith there is enough light for those who want to believe and enough shadows to blind those who don't. -Blaise Pascal Example 1 Use the first row of the partial Pascal's Triangle to fill in the blanks for the second row. a. 7 21 35 35 21 7 8 28 56 70 56 28 8 b. 5 10 10 5 6 15 20 15 6 1Use Pascal's Triangle to write the coefficients on the blanks to complete the binomial expansion. Simplify. a. (x+y) =1x3+ 3x y+3xy? +1y3 ( xty)' = x3 +3xy+3xy?+y3 b. ( x+ y) = 1x5 +5x*y+10x'y? + 10x?y3 + 5xy# + 1ys ( x+ y) =x+5x y+10x y2 +10xy3+5xx4+ c. (x+ y)* = 1x' + 4x y+6x?y? +4xy3+ 1y" ( xty )* = x* + 4x y+6x? y2 + 4xy3+ + Blaise Pascal Scat d. ( x + y ) =1x2+2xy+ 1yz Blaise Pascal was a mathematical genius who in his short, sickly life spanning 39 years actually ( x+ y)? = x2 +2xy+ y? devoted himself to religious endeavors more than mathematics. Fill in the blanks in the partial Pascal's Triangle. Even though Pascal did not invent the Triangle, because he made use of the array to develop many of the properties and uses of triangles, it became known as Pascal's Triangle. Among his many accomplishments, Pascal 2 invented a mechanical calculating machine 3 3 and was instrumental in laying the foundation for calculus. Since the calculating machine could do the work of 6 accountants, it was not accepted People feared it would cause unemployment. Because of people's negative reaction to his machine, Pascal rejected his interest in science and mathematics, devoting the rest of his life to God.The pattern for binomial expansions works for all types of binomials, including those with numbers in them. We need to be careful and precise with these expansions, showing every little step so we don't leave out a number. For each term of the expansion: (1) Write the coefficient from Pascal's Triangle, (2) Write the first term of the original binomial to the power of the binomial, (3) Write the second term of the original binomial to the zero power. (4) For all subsequent terms in the expansion, decrease the power of the first term by 1 from the previous power and increase the power of the second term by 1 from the previous power. Remember that any variable or number with an exponent of zero equals 1. Example 2 Expand the binomial and use Pascal's Triangle for the coefficients. Simplify. a. (x + 2) ' (x + 2) =(1)(x3) (20) +(3)(x2) (2') + (3)(x") (22) +(1)(23) (x + 2) = (1) (x3) (1) + (3) (x2) (2) +(3) (x)(4) +(1)(8) =x3+6x2+12x+8 b. (a + 3 )* (a +3)* =(1)(a)* (30)+(4)(a3)(3') +(6)(a?)(32)+(4)(a')(33) +(1)(a)(3" ) (a +3)* =(1)(a*)(1) + (4)(a3)(3) +(6)(a )(9) +(4)(a')(27) +(1)(1)(81) (a +3)" = a" +12a3 + 54a? +108a +81 When binomials have differences rather than sums, alternate signs beginning with plus. The signs will be +, -, +, -, etc. Everything else is the same as binomials with pluses between the terms. Example 3 a. (x- y)' ( x - y)' = (1)x y -(3) x 2y' +(3) x yz-(1) x0 3(x - y) = (1)x3(1) -(3)xy' + (3) xy2 -(1)(1)y3 = x3 - 3x y + 3xy? _y b. (y -2)* (y - 2)* = (1) ( y# ) (20 ) - (4) (y3) (2') + (6) ( 12) (22) -(4 ) (y') (23) + (1) ( 10) (2#) (y - 2)* = (1) ( y# ) (1) -(4) (y3) (2) + (6)(12) (4)-(4)(y') (8)+(1)(1) (16) (y -2)* = 14 -8y3+24y? -32y+16 Belief is a wise wager. Granted that faith cannot be proved, what harm will come to you if you gamble on its truth and it proves false? If you gain, you gain all; if you lose, you lose nothing. Wager, then, without hesitation, that He exists. -Blaise Pascal Blaise PascalAnswer the following questions. [1) Choose the correct numbers on the blanks in the Pascal's Triangle. 2 1 3 4 6 4 10 10 5 1 6 15 20 15 6 1 21 35 35 7 1\fW 2) Expand the binomial using Pascal's Triangle for the coefficients. Simplify. (at a)2 O ( x + a ) 2 = 2 + 2 x a + a O ( * + a) 2 = 2 + 2xa + a O ( ze + a )? = ne + axa + a O ( x + a) 2= 202 + 2xa + a-[ 3) Expand the binomial using Pascal's Triangle for the coefficients. Simplify. (2 - 3)3 O (2 - 3) 3 = 23 - 62+9 O (x - 3)3 - 9x2 +3x -9 O (x -3)3 - 23-9x2 +27x-27 O (2 - 3)3 = 2-92+27x-27[4) Expand the binomial using Pascal's Triangle for the coefficients. Simplify. (2 + 4 ) 4 O (2 + 4)4 = 24+16:3 + 96x2 + 256x + 256 O (x+ 4)$ = 2-9:+27x-27 O ( 2 + 4) 4 = 24 + 2xa + at O (x + 4)4 = 2 + 16x + 962+ 256x + 256 5) Expand the binomial using Pascal's Triangle for the coefficients. Simplify. (20 - 4) 4 O ( 20 - 4) 4 = 204 + 2 0 + at O ( 2 + 4) 4 = 20-92+272-27 O (2 - 4)4 = 2- 162 - 962 - 256x - 256 O (20 - 4)4 = 24-1623 + 96a2 - 256x + 256
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


