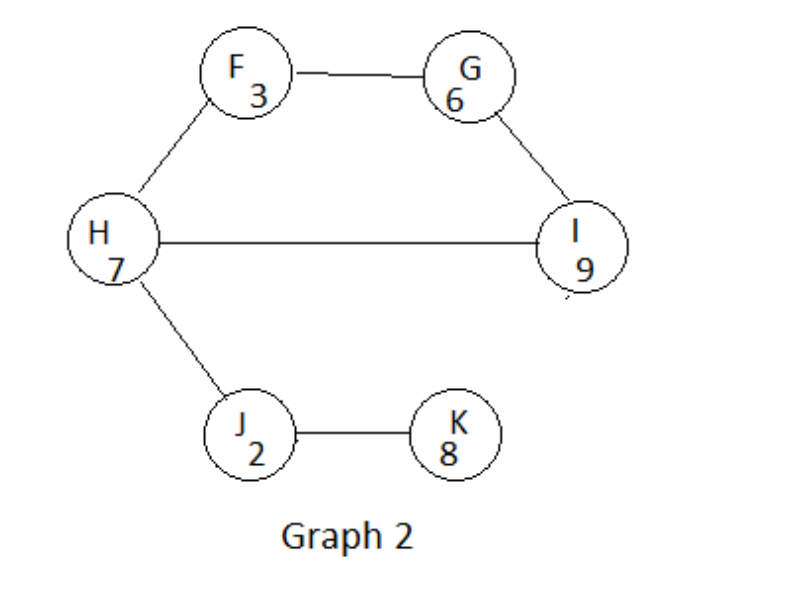
Graph 2 Consider trying to solve Best Independent Set using hill climbing in the following state space. State: Any set of vertices. Neighbors of state S : Either add one vertex to S or delete one vertex from S. Error function: Max(0,T( Total value of the vertices in S))+ sum of the cost of all edges that connect two vertices in S where the cost of an edge is considered to be the value of its lower end. For example, in graph 1, suppose S={A,C} and T=16. Edge AC is in G, value (A)=3, value (C)=6, so cost(AC)=3. So Error(S)=Max(0,(169))+3=10. What is the sequence of states encountered doing simple hill-climbing in this space, to solve this problem for Graph 2, starting from state {F,G,H,I,J} with a target of T=20