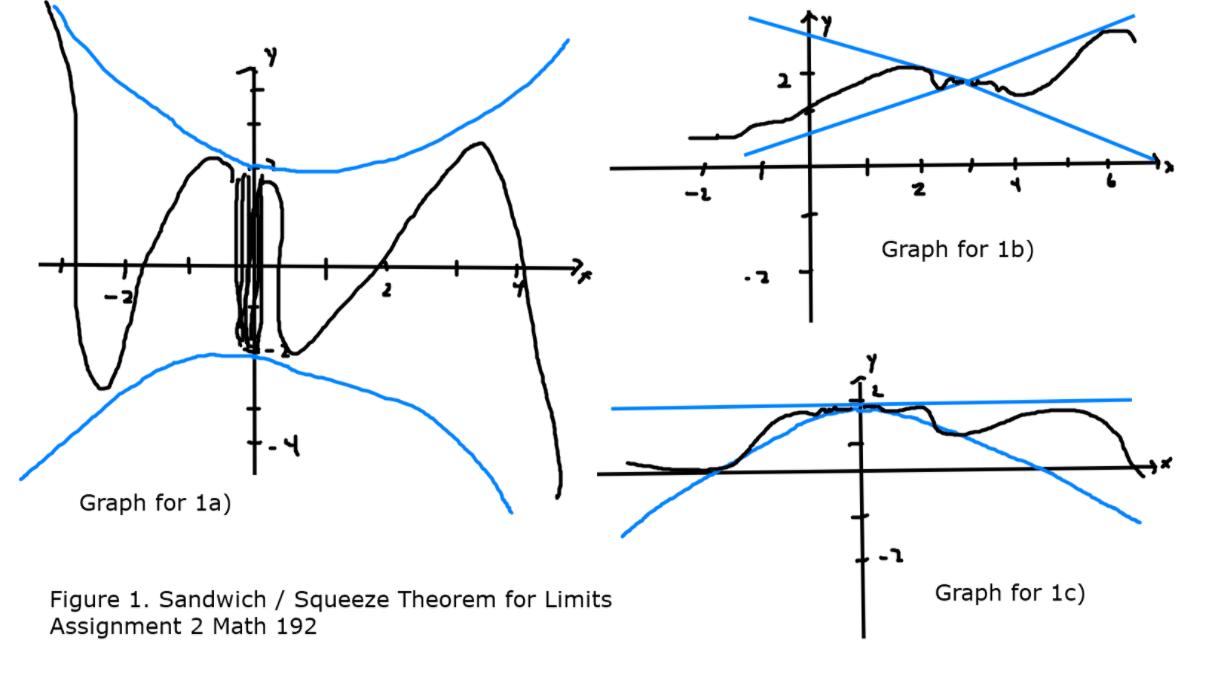
Question: Squeeze / Sandwich Theorem a) Consider a function f(x) that satisfies the following inequalities 2-|x| sf(x) s 2 cos x + sin x {



![192 c) Consider [Figure 2] in In graph 2a), there is a](https://dsd5zvtm8ll6.cloudfront.net/si.experts.images/questions/2021/03/60548256a9c01_ScreenShot20210319at6.52.00AM.png)
Squeeze / Sandwich Theorem a) Consider a function f(x) that satisfies the following inequalities 2-|x| sf(x) s 2 cos x + sin x { 2- |x| 3} g(x) Graph for 1b) Graph for la) Graph for 1c) Figure 1. Sandwich / Squeeze Theorem for Limits Assignment 2 Math 192 c) Consider [Figure 2] in In graph 2a), there is a representation of the function f(x) = sin((pi)/x) %3! while graph 2b) represents the function g(x) = x sin((pi)/x) both have an infinite number of oscillations within any finite interval around x=0; however these graphs are qualitatively different. Observe why the Squeeze / Sandwich Theorem applies to the graph of g(x) in 2b) but not to the graph of f(x) in 2a). Then explain why sin((pi)/x) and lim_{x-> 0} x sin ((pi/x) = 0 while lim_{x -> 0} sin (pi/x) does not exist QUESTION 20 Recall Heaviside function H(t) H(t) = (0, t = 0 For own paper graph H(t) and P(t) = H(t) - H(t - 1) %3D or P_a (t) = H(t) - H(t - a) %3D a) discuss discontinuities of these (also one-sided continuity) next we consider what we get when we multiply these by some other function try following 3 functions f(x), g(x) and h(x) f(x) = cos x g(x) = sin ((pi)x) h(x) = 9 - x^2 Sketch each of the following graphs; then answer the following questions H(x) f(x) H(x) g(x) P(x) f(x) P(x) g(x) P(x) h(x) which of these are continous? what conditions for F(x) are needed to ensure H(x) F(x) is continuous? to ensure P(x) F(x) is continuous?
Step by Step Solution
3.60 Rating (161 Votes )
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


