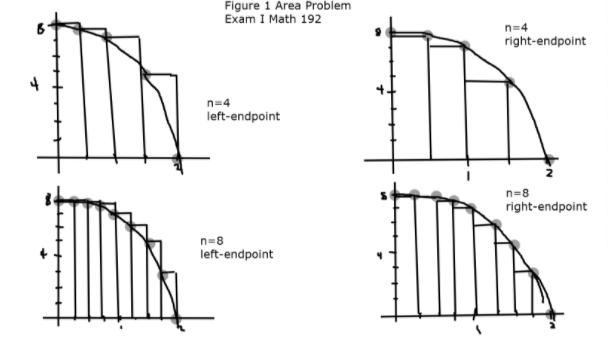
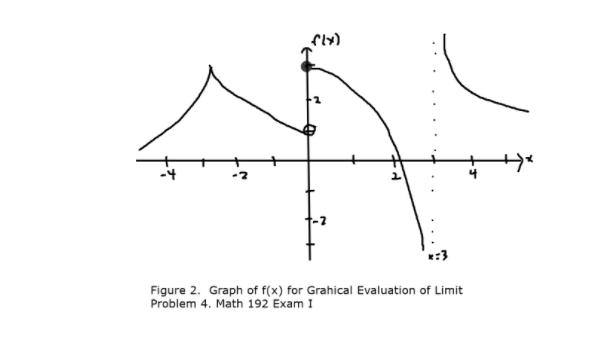
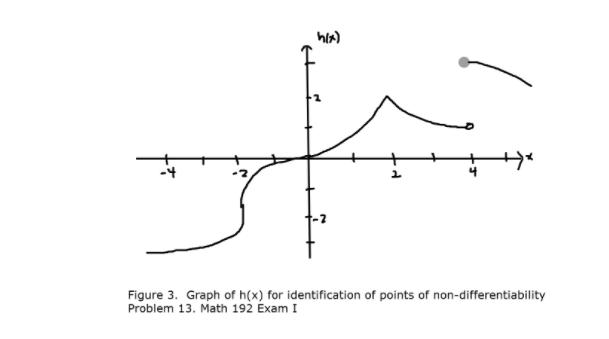
QUESTION 2 Area problem Find a Riemann sum approximation to the area in the first quadrant under the curve with equation y = 8 - x3 { y = 8 - x^3 } a. Find the left sum and right sum with n=4 rectangles. b. Find the left sum and right sum with n=8 rectangles. Figure 1 Area Problem Exam I Math 192 n=4 right-endpoint n=4 left-endpoint n=8 right-endpoint n=8 left-endpoint QUESTION 4 Graphical Evaluation of Limits For this problem consider the function f(x) defined by the graph given in [Figure 2] of the Additional Documents for Exam I. Evaluate each of the following limits, or state why the limit does not exist. a) lim f(x) X--3 { lim_(x -> - 3) f(x) } b) lim f(x) lim_(x -> 0} f(x) c) lim f(x) X+3 Figure 2. Graph of f(x) for Grahical Evaluation of Limit Problem 4. Math 192 Exam I QUESTION 13 differentiability Explain why a) and b) are not differentiable at the given point. x - 4 Xs-2 a) f(x) = | 4 - x | = {4- x2 - 2 2 { f(x) = |4 - x^2| = (x^2 - 4, x Figure 3. Graph of h(x) for identification of points of non-differentiability Problem 13. Math 192 Exam I