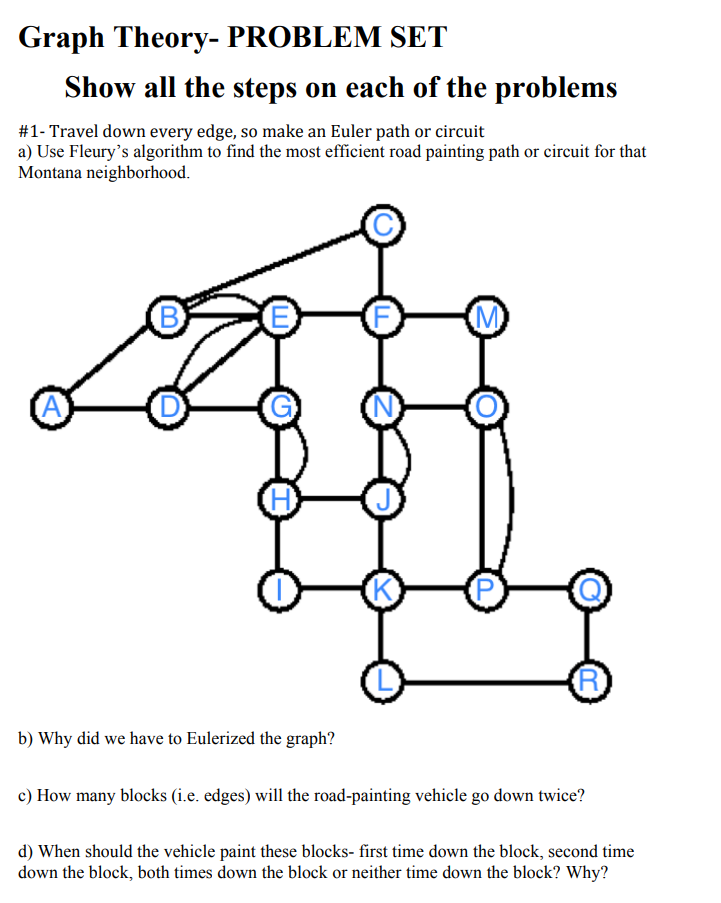
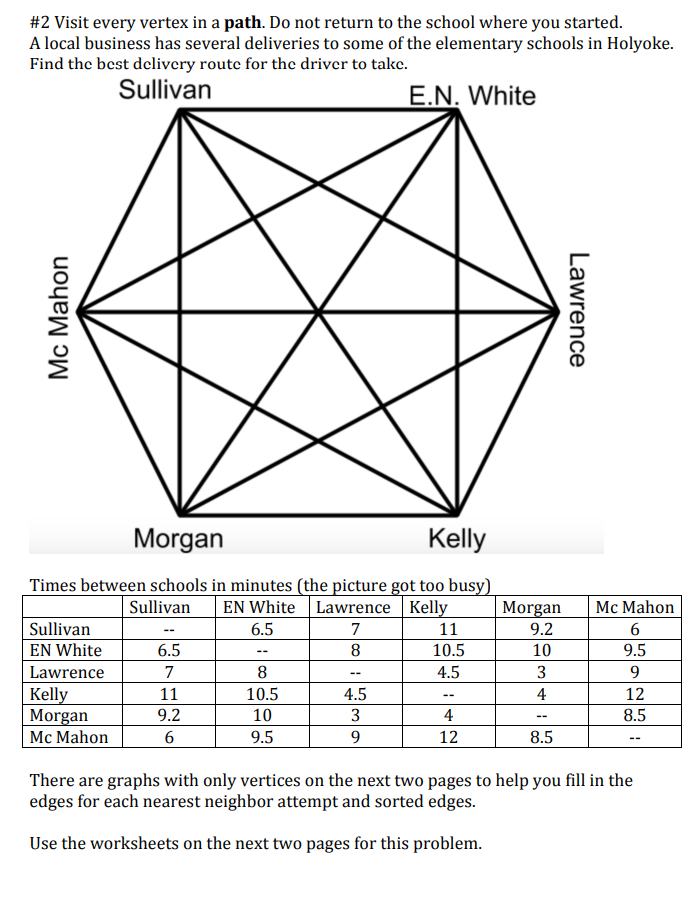
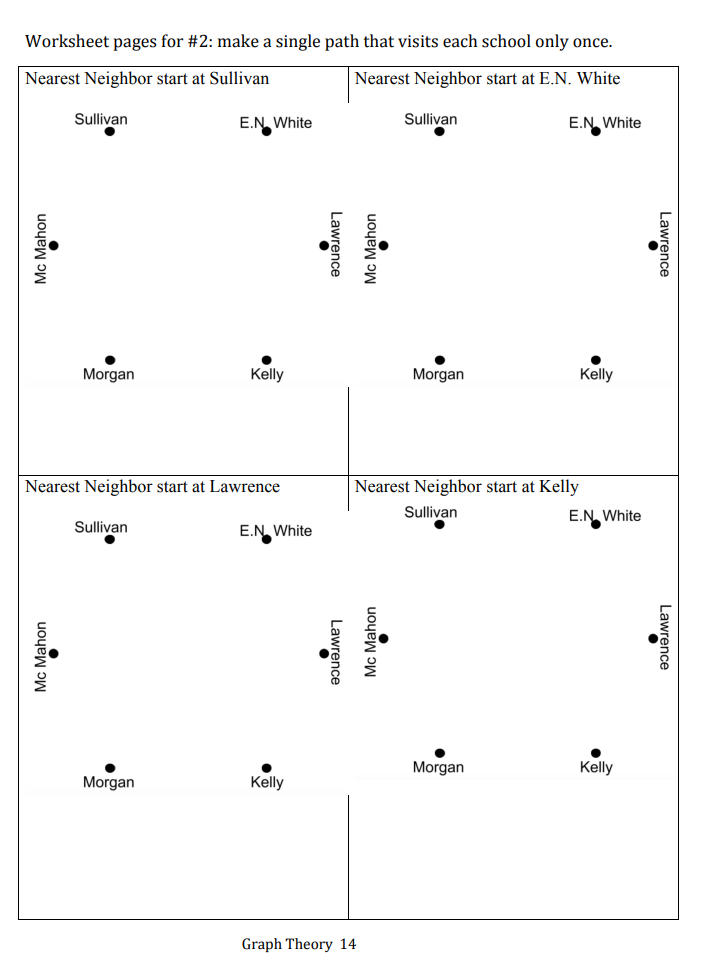
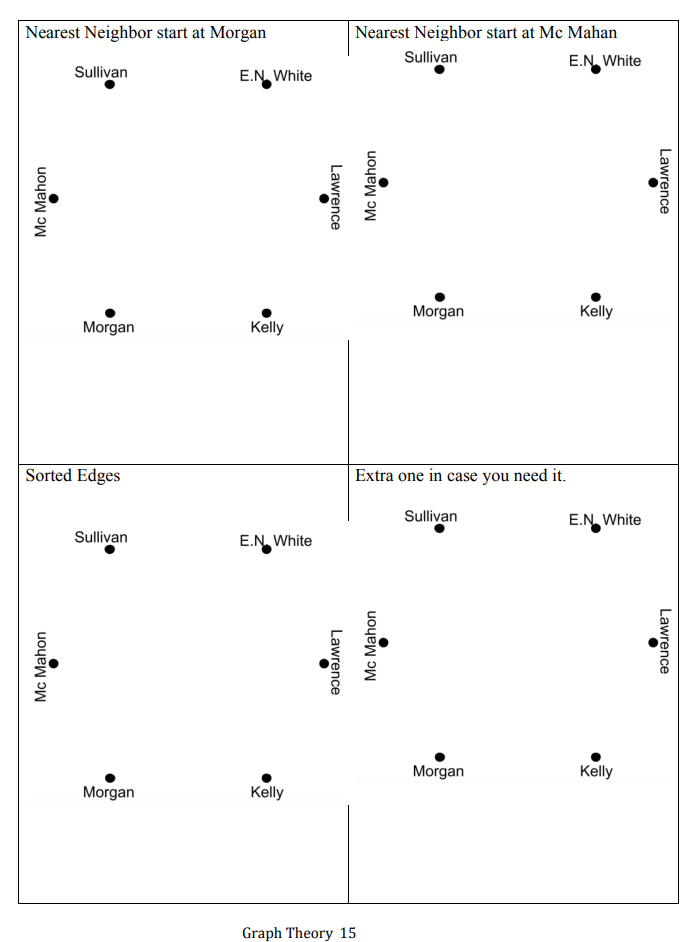
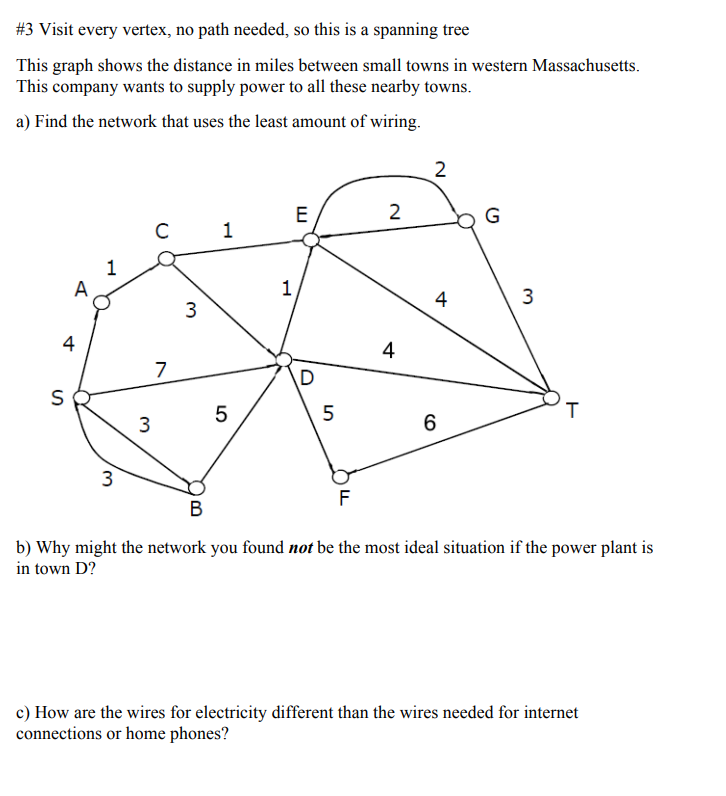
Graph Theory- VIDEO ASSIGNMENT There are 2 photos from Google maps of a section of Holyoke on the following pages. Use those maps to complete the assignment. Feel free to go on Google maps and take a closer look if that would be helpful. Type in Flats, Holyoke, MA then this is the area north of Appleton Street surrounded by the second level canal. You may also use street names in your explanations if you wish. For each graph make sure you mark each edge and each vertex. Remember if you need to go down a block twice then it needs two edges. If you do not need to go down a block at all, then do not include an edge there. Part 1: a) Create a graph that could be used to find the best path/circuit for the pothole checker who needs to slowly drive down every street once to look for potholes. Explain any choices you had to make and explain why you made the choices you made (For example: Did you skip a block? Did you double a block?) Note: Do NOT find the path/circuit, just draw the graph. b) Create a graph that could be used to find the best path/circuit for a walking mail carrier. Make sure you use both the satellite map and the road map. Explain any choices you had to make and explain why you made the choices you made. (For example: Did you skip a block? Did you double a block?) Note: Do NOT find the path/circuit, just draw the graph. Part 2: Create a FlipGrid video that includes the following: a) Show the two graphs you made in part 1 b) Explain why the two graphs are different showing specific examples c) Does an Euler path exist for either or both of these graphs? Why or why not? (Do NOT find it if it exists) d) Does an Euler circuit exist for either or both of these graphs? Why or why not? (Do NOT find it if it exists) Part 3: Submit digital versions of your two graphs on Moodle (a photo of your graph is fine) Grading Rubric: (In other words. what I will be looking for as I grade this assignment) Graph Theory 21 Graph Theory- PROBLEM SET Show all the steps on each of the problems #1- Travel down every edge, so make an Euler path or circuit a) Use Fleury's algorithm to find the most efficient road painting path or circuit for that Montana neighborhood. b) Why did we have to Eulerized the graph? c) How many blocks (i.e. edges) will the road-painting vehicle go down twice? d) When should the vehicle paint these blocks- first time down the block, second time down the block, both times down the block or neither time down the block? Why? #2 Visit every vertex in a path. Do not return to the school where you started. A local business has several deliveries to some of the elementary schools in Holyoke. Find the best delivery route for the driver to take. Times between schools in minutes (the picture got too busv) There are graphs with only vertices on the next two pages to help you fill in the edges for each nearest neighbor attempt and sorted edges. Use the worksheets on the next two pages for this problem. Worksheet pages for #2: make a single path that visits each school only once. Graph Theory 14 #3 Visit every vertex, no path needed, so this is a spanning tree This graph shows the distance in miles between small towns in western Massachusetts. This company wants to supply power to all these nearby towns. a) Find the network that uses the least amount of wiring. b) Why might the network you found not be the most ideal situation if the power plant is in town D ? c) How are the wires for electricity different than the wires needed for internet connections or home phones? Graph Theory- VIDEO ASSIGNMENT There are 2 photos from Google maps of a section of Holyoke on the following pages. Use those maps to complete the assignment. Feel free to go on Google maps and take a closer look if that would be helpful. Type in Flats, Holyoke, MA then this is the area north of Appleton Street surrounded by the second level canal. You may also use street names in your explanations if you wish. For each graph make sure you mark each edge and each vertex. Remember if you need to go down a block twice then it needs two edges. If you do not need to go down a block at all, then do not include an edge there. Part 1: a) Create a graph that could be used to find the best path/circuit for the pothole checker who needs to slowly drive down every street once to look for potholes. Explain any choices you had to make and explain why you made the choices you made (For example: Did you skip a block? Did you double a block?) Note: Do NOT find the path/circuit, just draw the graph. b) Create a graph that could be used to find the best path/circuit for a walking mail carrier. Make sure you use both the satellite map and the road map. Explain any choices you had to make and explain why you made the choices you made. (For example: Did you skip a block? Did you double a block?) Note: Do NOT find the path/circuit, just draw the graph. Part 2: Create a FlipGrid video that includes the following: a) Show the two graphs you made in part 1 b) Explain why the two graphs are different showing specific examples c) Does an Euler path exist for either or both of these graphs? Why or why not? (Do NOT find it if it exists) d) Does an Euler circuit exist for either or both of these graphs? Why or why not? (Do NOT find it if it exists) Part 3: Submit digital versions of your two graphs on Moodle (a photo of your graph is fine) Grading Rubric: (In other words. what I will be looking for as I grade this assignment) Graph Theory 21 Graph Theory- PROBLEM SET Show all the steps on each of the problems #1- Travel down every edge, so make an Euler path or circuit a) Use Fleury's algorithm to find the most efficient road painting path or circuit for that Montana neighborhood. b) Why did we have to Eulerized the graph? c) How many blocks (i.e. edges) will the road-painting vehicle go down twice? d) When should the vehicle paint these blocks- first time down the block, second time down the block, both times down the block or neither time down the block? Why? #2 Visit every vertex in a path. Do not return to the school where you started. A local business has several deliveries to some of the elementary schools in Holyoke. Find the best delivery route for the driver to take. Times between schools in minutes (the picture got too busv) There are graphs with only vertices on the next two pages to help you fill in the edges for each nearest neighbor attempt and sorted edges. Use the worksheets on the next two pages for this problem. Worksheet pages for #2: make a single path that visits each school only once. Graph Theory 14 #3 Visit every vertex, no path needed, so this is a spanning tree This graph shows the distance in miles between small towns in western Massachusetts. This company wants to supply power to all these nearby towns. a) Find the network that uses the least amount of wiring. b) Why might the network you found not be the most ideal situation if the power plant is in town D ? c) How are the wires for electricity different than the wires needed for internet connections or home phones