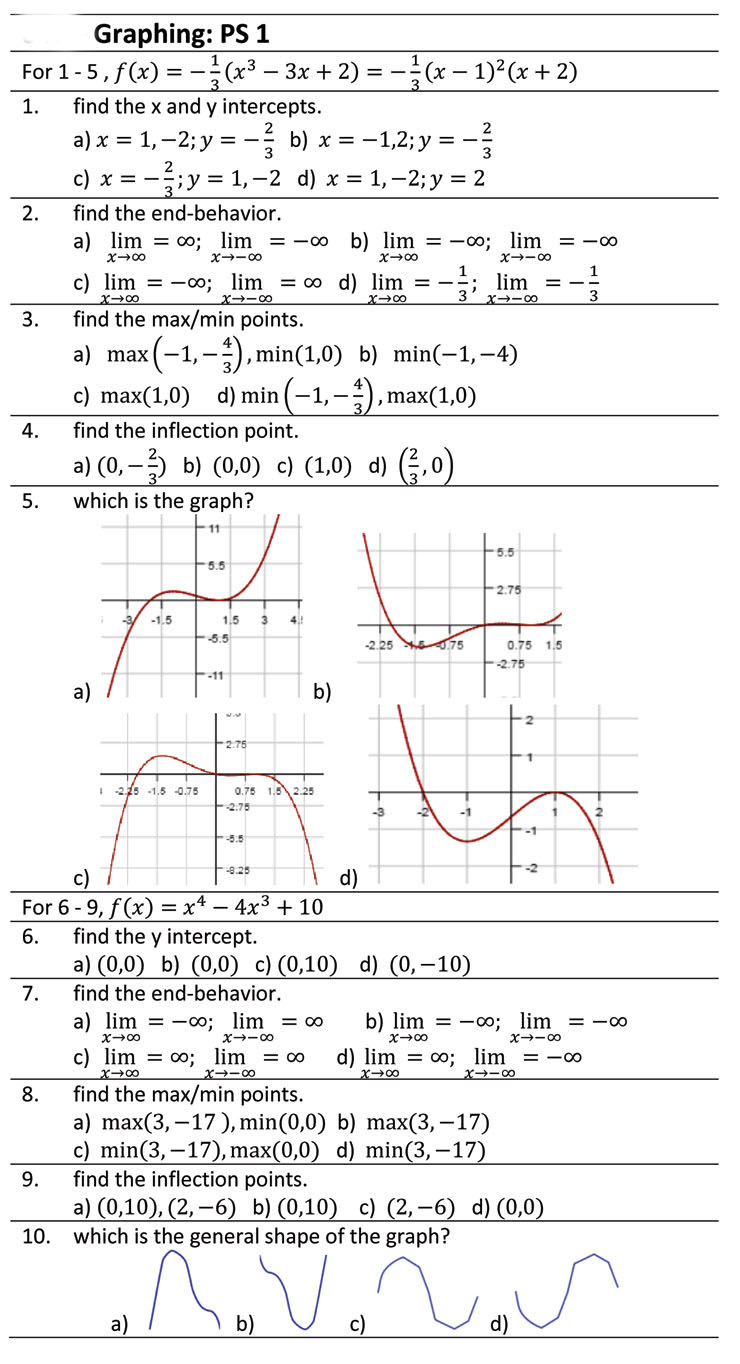
Graphing: PS 1 For 1 - 5 , f (x) = -= (x3 - 3x + 2) = -=(x -1)2(x+2) 1. find the x and y intercepts. a) x = 1, -2; y = - b) x = -1,2; y = - WIN c) x = -;y = 1, -2 d) x = 1, -2; y = 2 2. find the end-behavior. a) lim = co; lim = -co b) lim = -co; lim = -00 x-+00 X - -00 X-00 X- -00 c) lim = -co; lim = co d) lim = --; X-+00 X-2-00 lim = - X-+00 3 X--00 WIH 3. find the max/min points. a) max (-1, -2) , min(1,0) b) min(-1, -4) c) max(1,0) d) min (-1, - 2) , max(1,0) 4. find the inflection point. a) (0, - 2) b) (0,0) c ) (1,0) d ) ( ,0 ) 5. which is the graph? -5.5 -2.75 -1.5 1.5 -5.5 -2.25 15 0.75 0.75 1.5 -2.75 a) -11 b) 2.76 2.25 -1.5 -0.75 0.75 1.3 2.25 --2.75 -5.5 c) -8.2 d) For 6 - 9, f (x) = x4 - 4x3 + 10 6. find the y intercept. a) (0,0) b) (0,0) c) (0,10) d) (0, -10) 7. find the end-behavior. a) lim = -co; lim = 00 X -+ 00 X- -00 b) lim = -oo; lim = -00 X-co X - -00 c) lim = co; lim = 0o X-+00 X- 00 d) lim = co; lim = -co X-+00 X- -00 8. find the max/min points. a) max(3, -17 ), min(0,0) b) max(3, -17) c) min(3, -17), max(0,0) d) min(3, -17) 9. find the inflection points. a) (0,10), (2, -6) b) (0,10) c) (2, -6) d) (0,0) 10. which is the general shape of the graph? a) b) c)Optimization Problems 1. Find two positive numbers such that the product is 192 and the sum of the first plus three times the second is minimized. a) 32,6 b) 24, 8 c) 16.12 d) 8,24 2. A rectangle is inscribed in an isosceles triangle of height 10 and base 5. Find the dimension of the bottom of the rectangle so that area of the rectangle is maximized. (Use similar triangles.) 1D 5 a); b)3 c) 2 a); 3. Find the xvalue of the point on curve y = V3: 2 that is closest to (11,0). a)E bJE c) 10 d) 19 4. An open-top box is created bv folding a piece of 2 by 3 feet cardboard with four equal sized squares cut out of the corners. Find 1:, the side of one cut-out square so that the volume is maximized. {Use the quadratic formula; onlv one of the solutions makes sense given the dimensions of the cardboard.) a)1.27 b) .5 c) d] 0.4