Having trouble with this problem..

please help me with the steps to answer this problem in order

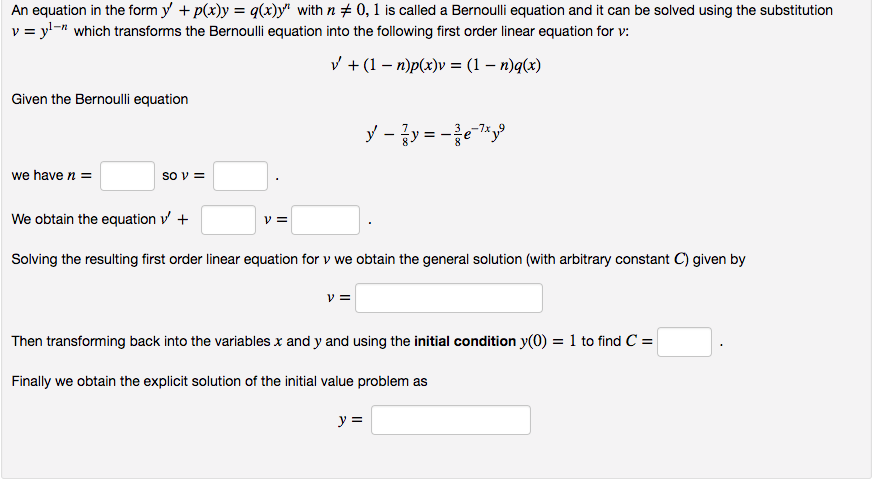
An equatlon in the form y' + p(x)y = q(x)y' wlth n 9'5 0, l is called a Bernoulli equatlon and it can be solved using the substitution 1: = yl'" which transforms the Bernoulll equation into the following rst order linear equation for v: v' +(1 n)p[x]v = {1 n}q(x} Given the Bernoulll equation WBHEUBH=I ISDV=I I. Weobtain the equation v" + I I v =I I . Solving the resulting rst order linear equation for v we obtain the general solution {with arbitrary oonetant C) glven by v =|. l Then transforming back into the variables x and y and uelng the Inltlal oondltlon y({}) = 1 to nd C = I I . Finally we obtain the expllcit solution of the Initial value problem as i=2 l