Hello! Could you please help me with this homework problem on fluid mechanics?

Here are some hints from my professor:

Thank you!

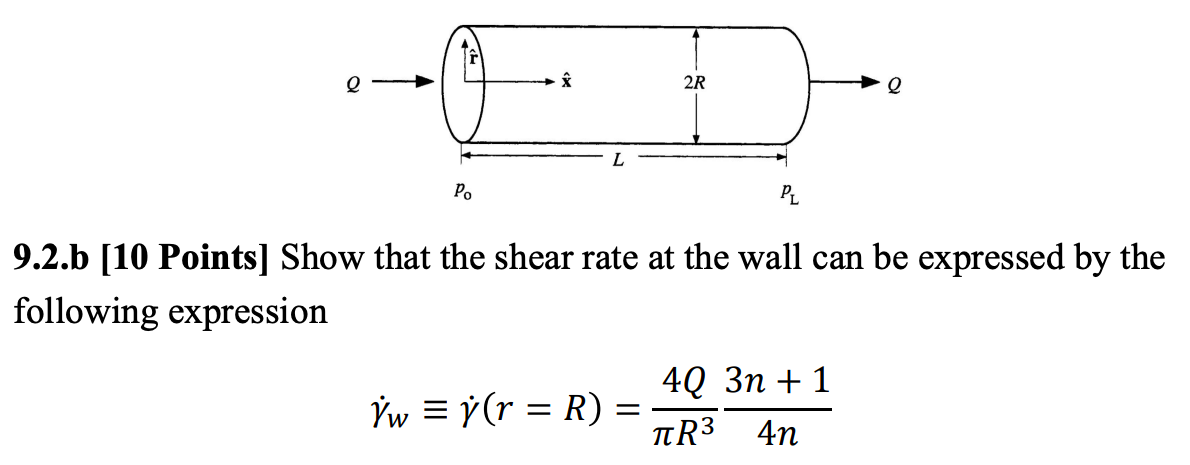
9.2.a [20 Points] Derive, starting from mass balance and momentum balance, the relationship between pressure drop (AP = Po - PL) and volume flow rate (Q) for the flow of a power-law fluid, with viscosity function: n(j) = min-1, through a long circular pipe with radius R and diameter D = 2R. = = Assume that (a) the flow is steady, laminar incompressible, and fully developed; (b) gravity is negligible; and (c) isothermal conditions. 2R e ED PO PL 9.2.b [10 Points] Show that the shear rate at the wall can be expressed by the following expression w = (r = R) = 4Q 3n +1 TR3 4n n = Type of fluid n(j) = mn-1 1 Dilatant (less common) = T = Bingham pseudoplastic Hints: A power-law fluid is a type of generalized Newtonian fluid (time-independent Non-Newtonian fluid) for which the shear stress, t, is given by where m is knows as the flow consistency index, n is known as the flow behavior index (dimensionless), and is the shear rate. In terms of the generalized Newtonian fluid model, we have = ) where the viscosity function follows n(j) = mn-1 Bingham plastic n> 1 Shear stress (T) (Pa] ilatant Newtonian 1 Pseudoplastic n 0). Define shear rate j = 0 as the magnitude of the velocity gradient. Within the framework of the GNF model, we have = Idux) Trx = n()* , j = = dvx dr dr For Hagen-Poiseuille Flow, vx(r) decreases as the radial distance r increases, and therefore the velocity gradient dvx(r)/dr