Hello,

I am working on a project concerning the Central Limit Theorem and I would like some help figuring something out.

We are asked to used some math package (could be Mathematica, or Python, FORTRAN, &c.) to investigate the central limit theorem. We are asked to use a random number generator from our chosen package, and "write a program (subroutine) that returns a random variable that takes on values between zero and one, but has a distribution function of your choice". Furthermore, we are asked to consider how 'a non-linear "map" of the [0,1] interval onto a [0,1] interval alters the distribution of an evenly-distributed x, and then ask yourself how to choose the "map" (i.e. a function, either an analytical function or a code) that produces a distribution function that you want to obtain.'

I have decided to try first to use the function 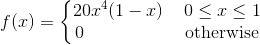for which I have the expected value 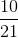and a variance of 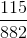. My question is: how do I implement the random number approach correctly to begin this problem? I can easily do a histogram plot and other analyses in Mathematica, Python, etc., but I am not sure how to begin. Specifically:

1. How do I pick the non-linear map that generates this distribution; and

2. Calculate the variance of the "new" distribution. Hint: what is the variance of the original random number generator?