... Help in solving this please

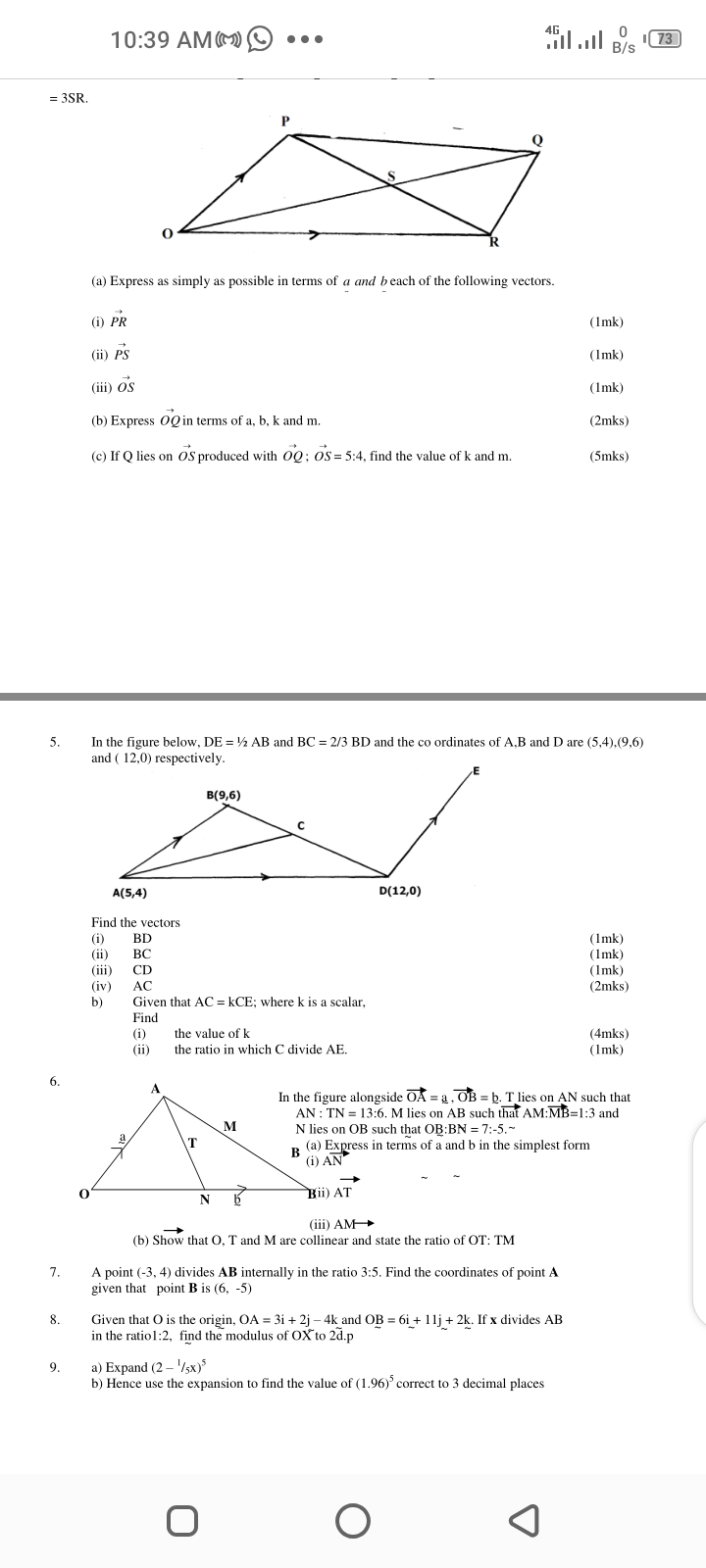
10:39 AM(M) .. . 9 73 Fill .Ill B/S 1. Vectors 2 1. In the figure below E is the mid point of BC. AD:DC = 3:2 and F is the meeting point of BD and AE 2 If AB = b and AC = c (a) Express the following in terms of b and c (i) BD (1mk) (ii) AE (2mks) (b) If BF = tBD and AF= n AE find the value of t and n. (5mks) (c) State the ratio of BD to BF. (1 mk) 2. In the figure below OA = a and OB = b. Points P and T divide OB and AB internally in the ration 2:3 and 1:3 respectively. Lines OF and AP meet at Q. T Q P Find in terms of a and b (1) OT (3mks) (ii) OP (1mk) (iii) AP (1mk) (iv) (5mks) If OQ = KOT and AQ = hAP where k and h are constants express OQ in two different ways and hence find the values of h and k. (10mks) 3. In the figure below OA =a, OB = band DB is parallel to OA. C is on AB extended such that AB: BC = 2:1 and that OA = 3DB. a) Express the vector BC in terms of a and b. (1mk) b) Show by vector methods that the points O, D and C are collinear. (3mks) 4. In the figure below OP = -a+b. OR = 2a-b. RQ = >kb+ - ma, where k and m are scalars 2PS = 3SR. O O10:39 AM(1) .. . 19 73 Hill .Ill B/S = 3SR. (a) Express as simply as possible in terms of a and beach of the following vectors. (1) PR (1mk) (ii) PS (1mk) (iii) os (1mk) (b) Express OQ in terms of a, b, k and m. (2mks) (c) If Q lies on OS produced with OQ; OS = 5:4, find the value of k and m. (5mks) 5. In the figure below, DE = 1/2 AB and BC = 2/3 BD and the co ordinates of A.B and D are (5,4),(9,6) and ( 12,0) respectively. B(9,6) A(5,4) D(12,0) Find the vectors BD (1mk) (ii) BC (1mk) (iii) CD (1mk) (iv) AC (2mks) b) Given that AC = kCE; where k is a scalar, Find (1) the value of k (4mks) ii) the ratio in which C divide AE. (1mk) 6 In the figure alongside OA = a , OB = b. T lies on AN such that AN : TN = 13:6. M lies on AB such that AM:MB=1:3 and M N lies on OB such that OB :BN = 7:-5. T R (a) Express in terms of a and b in the simplest form (i) AN Bii) AT (iii) AM- (b) Show that O, T and M are collinear and state the ratio of OT: TM A point (-3, 4) divides AB internally in the ratio 3:5. Find the coordinates of point A given that point B is (6, -5) 8 Given that O is the origin, OA = 3i + 2j - 4k and OB = 6i + 11j + 2k. If x divides AB in the ratio1:2, find the modulus of OX to 2d.p 9. a) Expand (2 - '/sx)5 b) Hence use the expansion to find the value of (1.96) correct to 3 decimal places O O