Help please

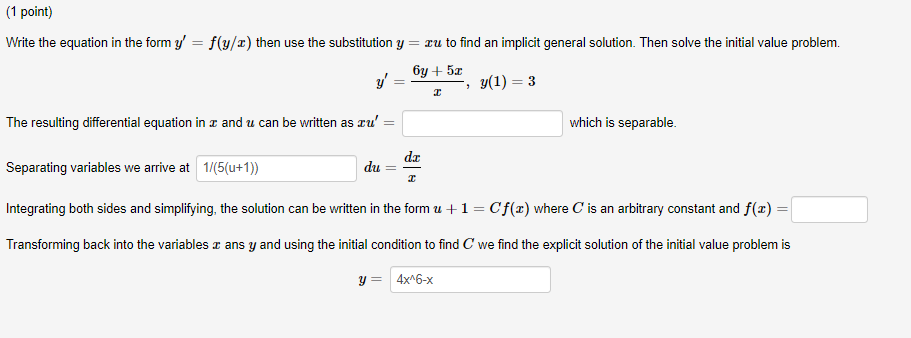
(1 point) In this problem we consider an equation in differential form M dx + N dy = 0. _ - 6(1 + In(x)) ) dx + (In(x) - 3y?)dy = 0 Find M. = 1/x N. = 1/x If the problem is exact find a function F(x, y) whose differential, dF(x, y) is the left hand side of the differential equation. That is, level curves F(x, y) = C, give implicit general solutions to the differential equation. If the equation is not exact, enter NE otherwise find F(x, y) (note you are not asked to enter C) F(x, y)(1 point} Write the equation in the town 9" = yfz) then use the substitution y 2 ms: to nd an implicit general solution. Then solve the initial value problem. By + 5: y' = = 9(1) = 3 z The resulting differential equation in a and u can be written as zu' = which is separable. Separating vanableswe anwe at 1i(5{u+1}} do = ? Integrating both sides and simplifying, the solution can be written in the form I: + 1 = Cm) where C is an arbitrary constant and x) = Transforming back into the 1wariables 3 ans y and using the initial condition to nd C we nd the explicit solution of the initial value problem is y = 4x\"6x