help please

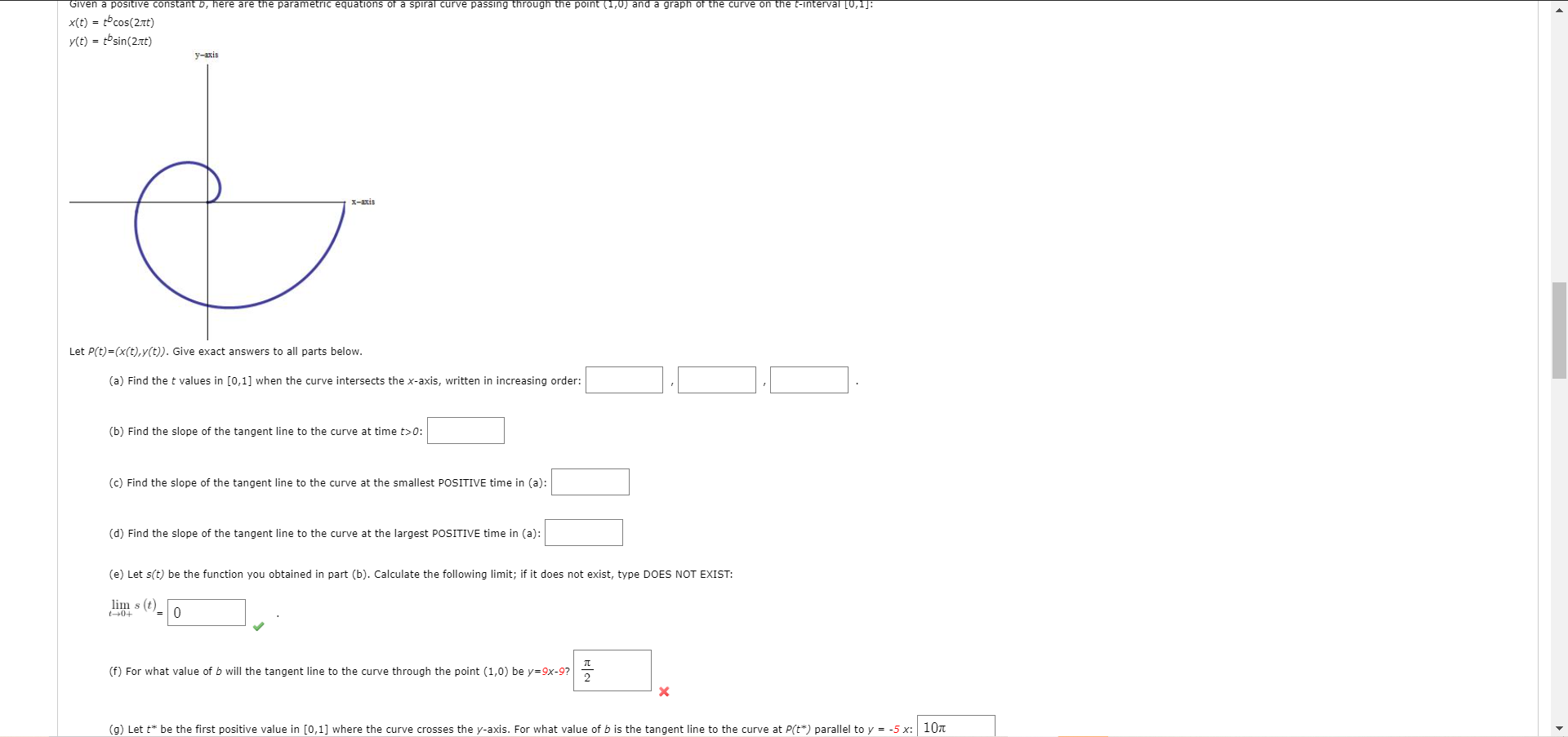
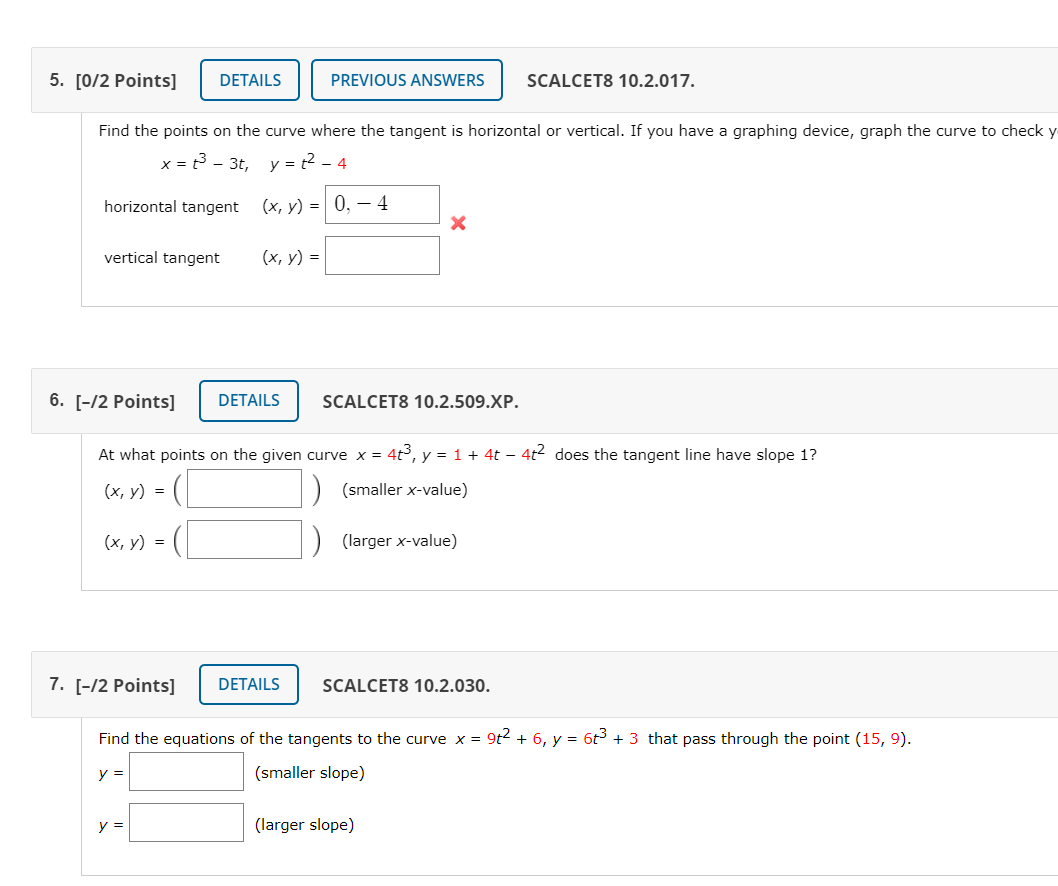
Given a positive constant x(t) = tbcos(2nt) y(t) = tosin(2nt) y-axis Let P(t)=(x(t),y(t)). Give exact answers to all parts below. (a) Find the t values in [0,1] when the curve intersects the x-axis, written in increasing order: (b) Find the slope of the tangent line to the curve at time t> 0: (c) Find the slope of the tangent line to the curve at the smallest POSITIVE time in (a): (d) Find the slope of the tangent line to the curve at the largest POSITIVE time in (a): (e) Let s(t) be the function you obtained in part (b). Calculate the following limit; if it does not exist, type DOES NOT EXIST: lim s (t)_ 0 (f) For what value of b will the tangent line to the curve through the point (1,0) be y=9x-9? X (g) Let t* be the first positive value in [0,1] where the curve crosses the y-axis. For what value of b is the tangent line to the curve at P(t*) parallel to y = -5 x: 1075. [0/2 Points] DETAILS PREVIOUS ANSWERS SCALCET8 10.2.017. Find the points on the curve where the tangent is horizontal or vertical. If you have a graphing device, graph the curve to check x = +3 - 3t, y = tz - 4 horizontal tangent (x, y) = 0, - 4 X vertical tangent ( x, y ) = 6. [-/2 Points] DETAILS SCALCET8 10.2.509.XP. At what points on the given curve x = 46, y = 1 + 4t - 4t does the tangent line have slope 1? (x, y) = () (smaller x-value) ( x, y ) = (larger x-value) 7. [-/2 Points] DETAILS SCALCET8 10.2.030. Find the equations of the tangents to the curve x = 9t- + 6, y = 6+ + 3 that pass through the point (15, 9). y = (smaller slope) (larger slope)