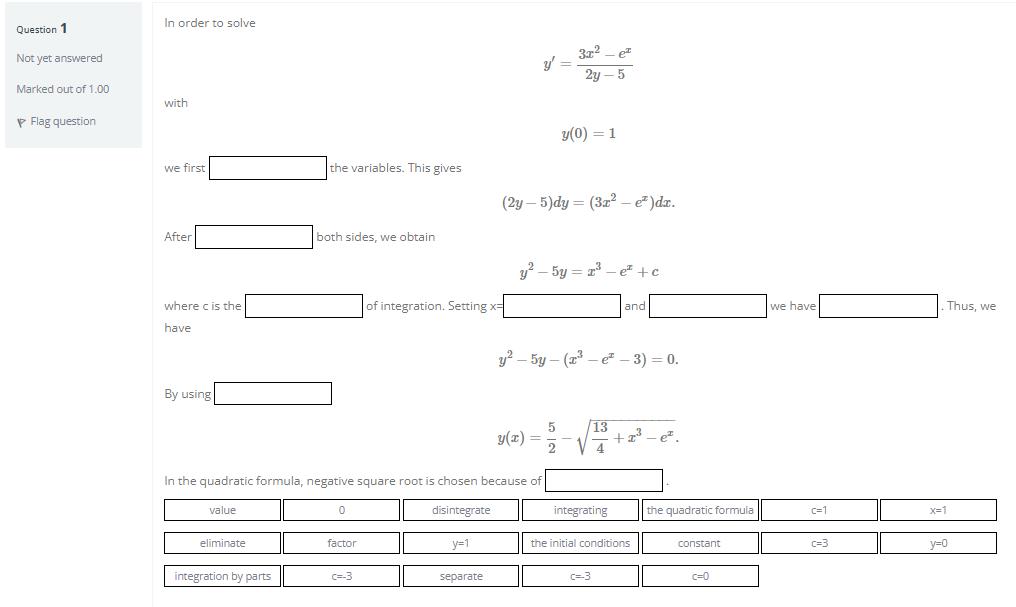
Question 1 Not yet answered Marked out of 1.00 Flag question In order to solve with y(0) = 1 we first (2y-5)dy = (3x e )dx. After y-5y = e +c of integration. Setting x= and where c is the have y-5y-(x-e- 3) = 0. By using 13 y(x)= 5 2 +2-e. In the quadratic formula, negative square root is chosen because of value 0 disintegrate y=1 eliminate factor integration by parts c=-3 separate the variables. This gives both sides, we obtain y' = 3r p 2y-5 integrating the initial conditions c=3 the quadratic formula constant c=0 we have c=1 c=3 Thus, we x=1 y=0