help solve questions 4c and 5

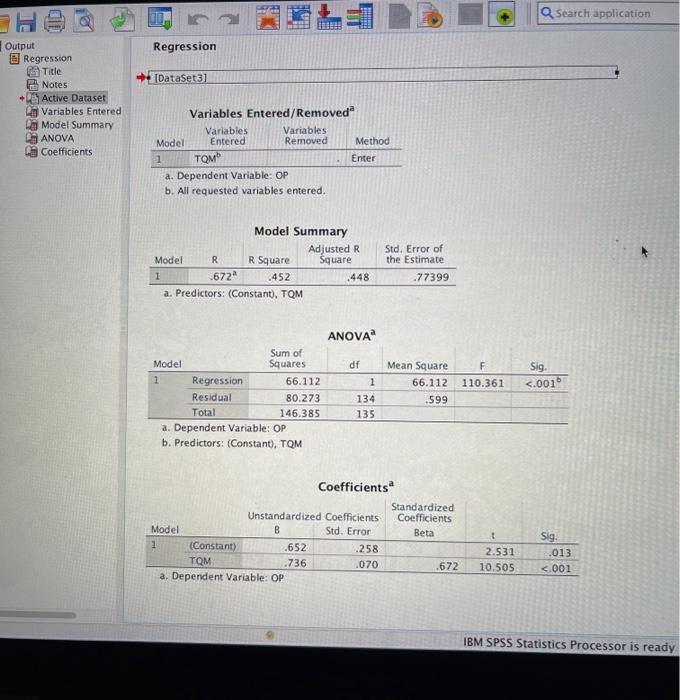
b. Complete a simple linear regression analysis with TQM as the independent variable and OP as the dependent variable with this command sequence [analyze, regression, linear, move OP in the dependent variable box, move TQM in the independent variable box, OK]. i. Note the R Square value in the second table. ii. Note the Beta value in the fourth table. iii. Note the vale in the Sig. column in the fourth table that corresponds to the Beta value. If the Sig. is .01 but .05, the Beta is not significantly different from zero (denoted with ns). c. Enter the R Square and the Beta in the model. Be sure to include the notation for significance (,ns) following the Beta value. 5. Interpret the results in the model answering the question: "Does TQM positively impact OP?" First interpret the Beta. Is it positive and significant at either the .01 or .05 level? Second, interpret the R2 value by moving the decimal to places to the right to turn it into a percentage. If the Beta is positive and significant, conclude that TQM does positively impact OP. Interpret the R2 percentage in this way: "The variation in TQM explains % of the variation in OP." Variables Entered/Removed a a. Dependent Variable: OP b. All requested variables entered. Model Summary a. rredictors: Constant, IUM b. Predictors: (Constant), TQM Coefficients a IBM SPSS Statistics Processor is ready Significance levels in regression analysis. Consider the following SPSS output. Note that the standardized coefficient (beta) for the MO to JT link is .278 with a computed significance level of .004 . Several folks incorrectly interpreted the significance level as . 05 instead of .01 . Once again, here are the decision criteria for determining the significance level of a regression coefficient: 1. If the computed significance level is less than or equal to .01 , the significance level is .01 (**) 2 If the computed significance level is greater than .01 but less than or equal to .05, the significance level is .05 (*) 3. If the computed significance level is greater than .05 , the coefficient is not significantly different from zero (not significant or ns) Now, take a look at the computed significance level of .004. Since .004 is less than .01 , the beta of .278 is significant at the .01 level. Let's try another example. Consider the following regression output. The computed significance level for the .036 beta is .725 . Since .725 is greater than .05 , the beta is not significant. The computed significance level for the .242 beta is .078 . Since .078 is greater than 05 , the beta is not significant. The computed significance level for the, 379 beta is .002 . Since .002 is less than .01 , the beta is significant at the .01 level