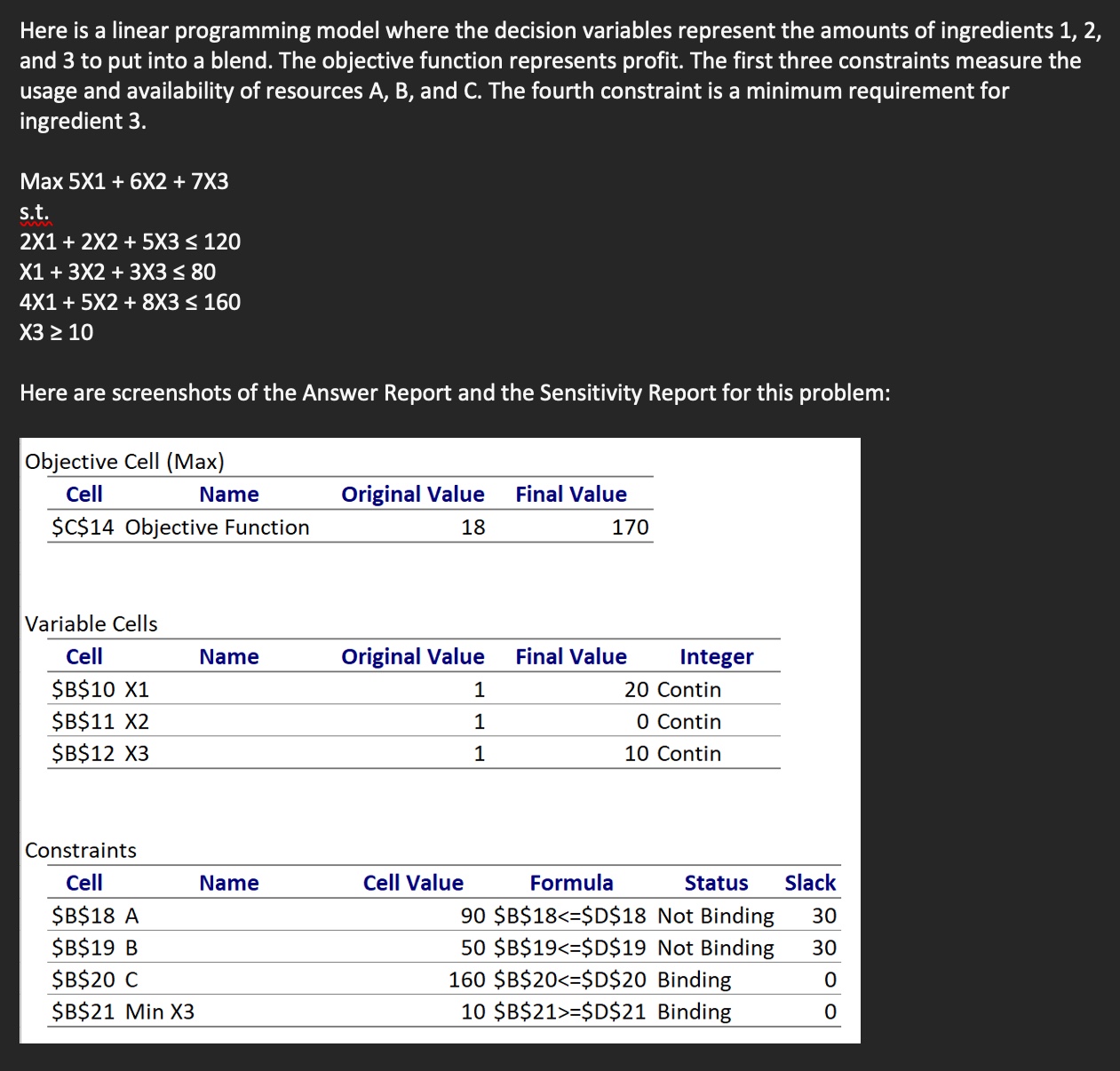
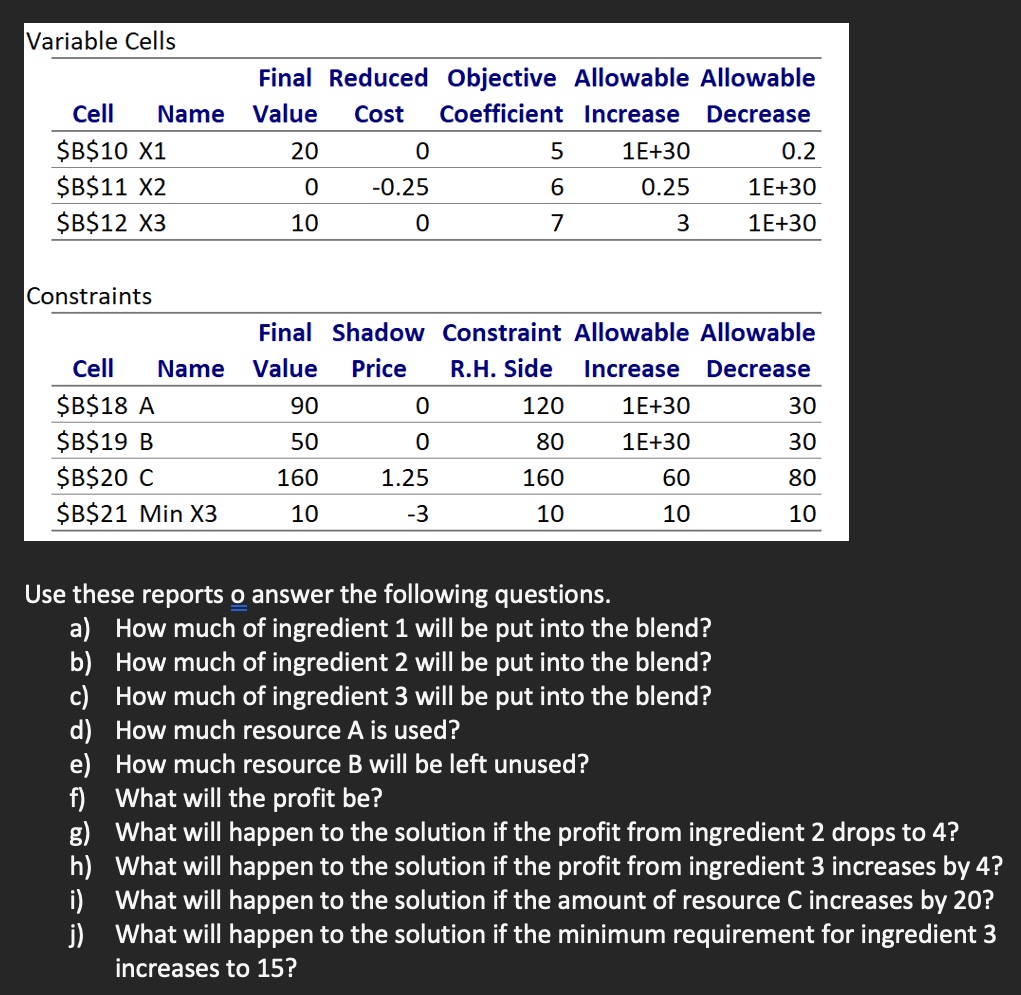
Here is a linear programming model where the decision variables represent the amounts of ingredients 1,2 , and 3 to put into a blend. The objective function represents profit. The first three constraints measure the usage and availability of resources A, B, and C. The fourth constraint is a minimum requirement for ingredient 3. \\[ \\begin{array}{l} \\operatorname{Max} 5 X 1+6 X 2+7 X 3 \\\\ \\text { s.t. } \\\\ 2 X 1+2 X 2+5 X 3 \\leq 120 \\\\ X 1+3 X 2+3 X 3 \\leq 80 \\\\ 4 X 1+5 X 2+8 X 3 \\leq 160 \\\\ X 3 \\geq 10 \\end{array} \\] Here are screenshots of the Answer Report and the Sensitivity Report for this problem: Objective Cell (Max) Variable Cells Constraints Variable Cells Constraints Use these reports o answer the following questions. a) How much of ingredient 1 will be put into the blend? b) How much of ingredient 2 will be put into the blend? c) How much of ingredient 3 will be put into the blend? d) How much resource \\( A \\) is used? e) How much resource \\( B \\) will be left unused? f) What will the profit be? g) What will happen to the solution if the profit from ingredient 2 drops to 4 h) What will happen to the solution if the profit from ingredient 3 increases i) What will happen to the solution if the amount of resource \\( \\mathrm{C} \\) increases by j) What will happen to the solution if the minimum requirement for ingredie increases to \\( 15 ? \\)