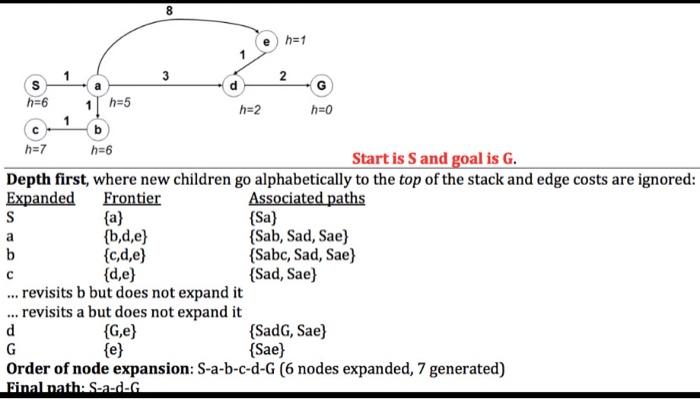
Here is pseudocode for a general search algorithm. It accepts a problem (e.g., Farmer), a structure (e.g., a list or a heap), and searches for a solution by using select to remove a node from the frontier. Supersearcher(problem, structure, select) node + initial-state(problem) reached frontier + new instance of structure that contains only node Until frontier = 0 do current select(frontier) children - generate children of current for child in children if ISGOAL(state(child)) = true then return child else if child reached then add child to reached add child to frontier return failure -Copy Supersearcher. Insert pseudocode that counts and returns the number of nodes generated, whether or not it finds a solution. -Copy Supersearcher again. Insert pseudocode that counts and returns the number of nodes expanded, whether or not it finds a solution. -Copy Supersearcher again. Insert pseudocode that calculates and returns the maximum search tree depth. -Copy Supersearcher again. Insert pseudocode that returns the total time required to search. Expanded nodes are ones that's children are generated and generated nodes are ones that come up in the search associated paths but are not necessarily expanded. The picture below shows how expanded and generated nodes are calcuated during dfs. 8 n=1 b 2 h=6 h=5 h=2 h=0 h=7 h=6 Start is S and goal is G. Depth first, where new children go alphabetically to the top of the stack and edge costs are ignored: Expanded Frontier Associated paths S {a} (Sa) {b,d,e) {Sab, Sad, Sae) b {c,d,e) {Sabc, Sad, Sae) {d,e) {Sad, Sae) ... revisits b but does not expand it ... revisits a but does not expand it d {G,e) {Sad, Sae) G {e} {Sae) Order of node expansion: S-a-b-c-d-G (6 nodes expanded, 7 generated) Final nath: S-a-d-G a